How to prove this vector equation?

[Ganesh Ujwal]

Proving $||\vec{a}+\vec{b}|| = ||\vec{a}-\vec{b}|| \iff \vec{a} \perp \vec{b}$

Have some non-null $\vec{a}$ and $\vec{b}$.

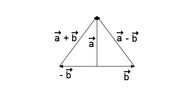
View attachment 3776

I am trying to prove this to no avail:

$$||\vec{a}+\vec{b}|| = ||\vec{a}-\vec{b}|| \iff \vec{a} \perp \vec{b}$$

-----

If we start with

$$||\vec{a}+\vec{b}|| = ||\vec{a}-\vec{b}|| \implies \vec{a} \perp \vec{b}$$

Our hypothesis is

$$||\vec{a}+\vec{b}|| = ||\vec{a}-\vec{b}||$$

Which tells us that both horizontal sides of this triangle have the same length, so we got an isosceles triangle. Not sure what to make out of that though.

Anyway, the hypothesis is equivalent to

$$\sqrt{(\vec{a} + \vec{b})\cdot (\vec{a} + \vec{b})} = \sqrt{(\vec{a} - \vec{b})\cdot (\vec{a} - \vec{b})}$$

From here, i don't know how to proceed?

 

[Opalg]

Anyway, the hypothesis is equivalent to

$$\sqrt{(\vec{a} + \vec{b})\cdot (\vec{a} + \vec{b})} = \sqrt{(\vec{a} - \vec{b})\cdot (\vec{a} - \vec{b})}$$

From here, i don't know how to proceed?

Square both sides: $(\vec{a} + \vec{b})\cdot (\vec{a} + \vec{b}) = (\vec{a} - \vec{b})\cdot (\vec{a} - \vec{b})$. Now multiply out those brackets and simplify the resulting equation, to end up with $\vec{a}\cdot \vec{b} = 0$.