kenny1999
- 235
- 5
- Homework Statement
- absolute value
- Relevant Equations
- inequality
see attached image, it asks to repesent it in x-graph
constant "a" isn't conditioned.
Do I need to separate it into a few cases of the constant a and represent each in one x-graph?
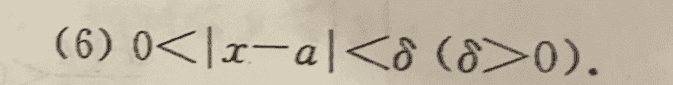
constant "a" isn't conditioned.
Do I need to separate it into a few cases of the constant a and represent each in one x-graph?
Last edited by a moderator: