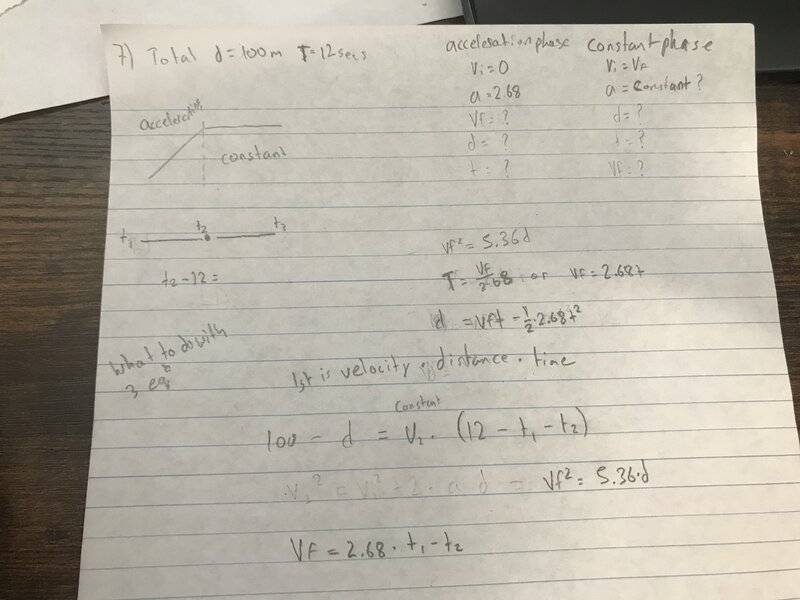How to Solve a 100m Dash Kinematics Problem with Unknown Acceleration?

[Mjusttheletter]

Homework Statement

In the 100m dash, a sprinter accelerates from rest to top speed with an acceleration whose magnitude is 2.68m/s^2. After achieving top speed, he runs the remainder of the race without speeding up or slowing down. If the total race is run in 12secs how far does he run during the acceleration phase?

Relevant Equations

two phases I don't really know what to put here?

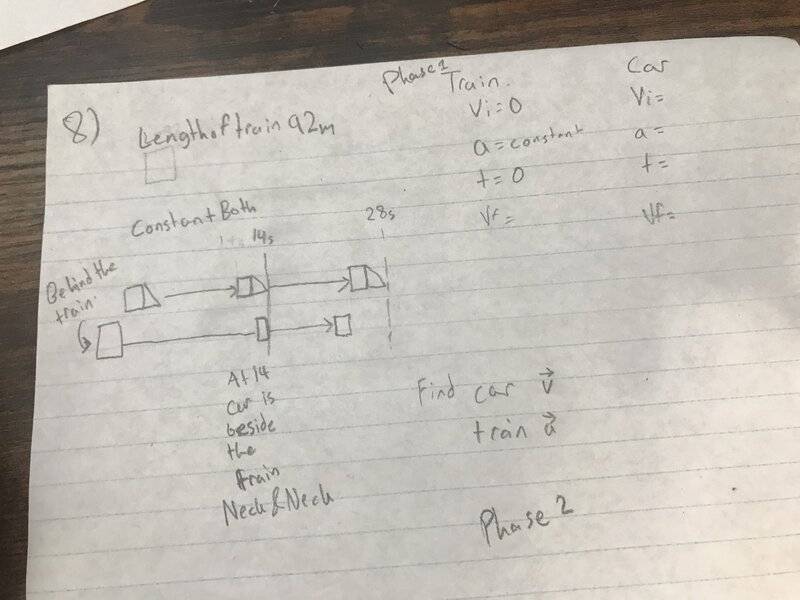
So what I have done is that on question 7 I know he is accelerating to constant my knowns are that it is from initial and acceleration is given so I have that for my first phase the second phase is that Your vfinal is your new initial for it and acceleration is the constant but you don't know what it is what I have done is got three equations and now I don't know what to do with them I also need help with 8 so I inserted my attempt but I don't know where to start a hint be nice or a solution I wouldn't mind both, to be honest.

 

[PeroK]

It looks like the first thing you did was start to draw a velocity against time graph. Given the the distance in this case is the area under that graph, can use use this to solve the problem using elementary geometry?

 

[Mjusttheletter]

It looks like the first thing you did was start to draw a velocity against time graph. Given the the distance in this case is the area under that graph, can use use this to solve the problem using elementary geometry?

Wait I'm confused so the total distance is 100m how could you use that with the area under the graph with only knowing the acceleration

 

[PeroK]

Wait I'm confused so the total distance is 100m how could you use that with the area under the graph with only knowing the acceleration

It might be easier to use the geometry to guide you. Rather than only trying things algebraically.

That said, you may have to aim for a quadratic in $t_1$ or $v$.

Note that $v$ is constant for the second phase of the motion.

 

[vela]

Wait I'm confused so the total distance is 100m how could you use that with the area under the graph with only knowing the acceleration

You have the freedom to set $t_1=0$.

Let's call the speed the runner attains $v$. What are the area of the triangle and rectangle in terms of $v$, $t_1$, and $t_2$?

 

[Mjusttheletter]

It might be easier to use the geometry to guide you. Rather than only trying things algebraically.

That said, you may have to aim for a quadratic in $t_1$ or $v$.

Note that $v$ is constant for the second phase of the motion.

where do you start the quadratic I tried it but I still am kind of lost.

 

[PeroK]

where do you start the quadratic I tried it but I still am kind of lost.

Can you post your diagram? There are two areas: a triangle for the acceleration and a rectangle for the constant velocity. There are two times $t_1$ and $t_2$, adding to a total of $T = 12s$, say. And, there's a maximum speed $v$ that is constant for the second phase.

And, if we call the areas $d_1$ and $d_2$, then $d_1 + d_2 = d = 100m$.

 

[Mjusttheletter]

Can you post your diagram? There are two areas: a triangle for the acceleration and a rectangle for the constant velocity. There are two times $t_1$ and $t_2$, adding to a total of $T = 12s$, say. And, there's a maximum speed $v$ that is constant for the second phase.

And, if we call the areas $d_1$ and $d_2$, then $d_1 + d_2 = d = 100m$.

 

[PeroK]

Okay, but $t_2 \ne 12 s$. The time of $12s$ is the total for the race. So, $t_1 + t_2 = 12s$.

I wouldn't worry about $v_i$ and $v_f$. You have a single maximum speed $v$ at the end of the acceleration phase, which is sustained for the second phase.

To give you a bit of help, the distances are $d_1 = \frac 1 2 vt_1$ and $d_2 = vt_2$. Can you make progress from there?

Note that $v = at_1$.

 

[Mjusttheletter]

Okay, but $t_2 \ne 12 s$. The time of $12s$ is the total for the race. So, $t_1 + t_2 = 12s$.

I wouldn't worry about $v_i$ and $v_f$. You have a single maximum speed $v$ at the end of the acceleration phase, which is sustained for the second phase.

To give you a bit of help, the distances are $d_1 = \frac 1 2 vt_1$ and $d_2 = vt_2$. Can you make progress from there?

Note that $v = at_1$.

can you explain a little how would it plug in or work out with the three equations that's the part I got stuck on with how it would work

 

[Lnewqban]

Your graph should be velocity versus time.
You will have a line starting at the origin with a slope equal to the acceleration (y=mx).
You will have a second line, horizontal, representing top speed.
The point at which both lines intersect represent the time at which there is a transition from accelerated rectilinear movement to constant velocity.

Now, the total distance of 100 meters is the area under the sloped line (t=0 to t=transition time) plus the area under the horizontal line (t=transition time to t=12 seconds).
Area triangle + Area rectangle = 100

Resolving that, you will have a quadratic equation and the value of the transition time.
With that, you can calculate how far the sprinter run during the acceleration phase.

 

[PeroK]

can you explain a little how would it plug in or work out with the three equations that's the part I got stuck on with how it would work

There are three related unknowns $v$, $t_1$ and $t_2$. You need to eliminate two of these from your equations. "Elimination" is an important algebraic idea. You need to understand this idea.

First, we have $t_1 + t_2 = T = 12s$. So, we may replace $t_2$ by $T - t_1$ in our equations. Second, $v = at_1$, so we may replace $v$ by $at_1$ in our equations.

That leaves $t_1$ as the only unknown in our equation(s). And, in fact, you should be left with a quadratic equation in $t_1$, which you can solve for $t_1$.

 

[Amphibia]

Question 8 you should know that the car displacement is 98 then goes back to zero displacement in the 2nd

 

[chwala]

Was this problem solved by op?

 

[kuruman]

Was this problem solved by op?

Is this a rhetorical question?

If it isn't, define "solved by OP". OPs post on this forum seeking help for solving problems that they can't solve on their own. Obviously, this OP got help with this problem. If you are really asking "Did OP reach a final answer to this problem with the help that was given?", one can only shrug and say "that cannot be known because OP hasn't come back yet to inform us."