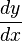How to solve a differential equation using substitution?

[find_the_fun]

Solve the DE using an appropriate substitution.

$$(x-y)dx+xdy=0$$

First step is to determine the substitution. I was told for homogeneous ODEs to always make the substitution y=ux but the substitution u=x-y looks better.

Let u = x-y then u'=-y' which means y'=-u'
rewrite the original equation x-y+xy'-o
now plugging in u and u' gives u+x(-u')=0 which gives x du = -u dx and integrating gives xu=-ux which doesn't make any sense.

 

[MarkFL]

I would first rewrite the ODE as:

$$\d{y}{x}=\frac{y}{x}-1$$

Using the substitution $$v=\frac{y}{x}$$, we then get:

$$\d{v}{x}=-\frac{1}{x}$$

Can you proceed?

 

[find_the_fun]

I would first rewrite the ODE as:

$$\d{y}{x}=\frac{y}{x}-1$$

Using the substitution $$v=\frac{y}{x}$$, we then get:

$$\d{v}{x}=-\frac{1}{x}$$

Can you proceed?

I don't really know what the overall procedure is when it comes to substitution. Wikibooks states the procedure is

1. Take a term of the equation and replace it with a variable v. The key is that the new variable must cover all instances of the variable y. Otherwise substitution would not help.
2. Solve for
   
   in terms of
   
   and
   
   . To do this, take the equation
   
   where
   
   is the term you replaced and take its derivative.
3. Plug in
   
   and solve for
   
   .
4. Plug
   
   into the original term replaced, and solve for
   
   .

I'm unclear on the first step. How do you know what the substitution should be? What made you say let [math]v=\frac{y}{x}[/math]? EDIT: in step 1 they say "take a term", what's a term?

 

[Prove It]

I don't really know what the overall procedure is when it comes to substitution. Wikibooks states the procedure is

1. Take a term of the equation and replace it with a variable v. The key is that the new variable must cover all instances of the variable y. Otherwise substitution would not help.
2. Solve for in terms of and . To do this, take the equation where is the term you replaced and take its derivative.
3. Plug in and solve for .
4. Plug into the original term replaced, and solve for .

I'm unclear on the first step. How do you know what the substitution should be? What made you say let [math]v=\frac{y}{x}[/math]? EDIT: in step 1 they say "take a term", what's a term?

A term is simply a part of the function.

It comes from experience knowing to substitute v = y/x. In general, if it CAN be written like a function of y/x, when the substitution should be valid and give you a separable DE in terms of v and x.

 

[find_the_fun]

Ok I think I'm starting to understand. One attempt I made led me to the wrong answer, where did I go wrong?

$$(x-y)dx + xdy=0$$
let $$y =ux$$ then $$dy=x du + u dx$$
Plugging in $$(x-ux)dx+x^2du+xu dx = 0 $$
simplifies to [math]x^2du+xdx=0[/math]
so one solution is $$x=0$$ (or should it be y?)

Now we can factor out an x so $$x(x du + dx)=0 \implies xdu+dx=0
$$

Now can we just integrate so [math]\int x du + \int dx = xu+x+C=0[/math] putting back in $$u=\frac{y}{x}$$ gives $$x \frac{y}{x} +x+C \implies y=-x+C$$ but the answer key has [math]y+xln|x|=xC[/math]

 

[Siron]

Your substitution is correct, but at the end you do some invalid steps.
We need to solve $xdu+dx=0$. Separable of the variables yields
$$-xdu = dx \Leftrightarrow -du = \frac{dx}{x} \Leftrightarrow -u = \ln|x|+C$$
Back-substitution gives
$$\frac{-y}{x}=\ln|x|+C$$
and hence the solution is $-y = x \ln|x|+Cx \Rightarrow y + x \ln|x|=Cx$.

 

[find_the_fun]

Your substitution is correct, but at the end you do some invalid steps.
We need to solve $xdu+dx=0$. Separable of the variables yields
$$-xdu = dx \Leftrightarrow -du = \frac{dx}{x} \Leftrightarrow -u = \ln|x|+C$$
Back-substitution gives
$$\frac{-y}{x}=\ln|x|+C$$
and hence the solution is $-y = x \ln|x|+Cx \Rightarrow y + x \ln|x|=Cx$.

Can you point out which steps are invalid so I don't repay them again.

 

[topsquark]

Hint:
Take a closer look at [math]\int xu~du[/math]. Is x a constant with respect to u?

-Dan

 

[find_the_fun]

Hint:
Take a closer look at [math]\int xu~du[/math]. Is x a constant with respect to u?

-Dan

No, x is a variable used by u. So what does that matter? And where did I use [math]\int xu~du[/math]?

 

[Siron]

As Topsquark already said, Take a closer look at your post:

Now can we just integrate so [math]\int x du + \int dx = xu+x+C=0[/math]

You claim: $\int x du = x u$, which means that you've treated $x$ as a constant. But the integral is with respect to $u$ and $u$ is a function of $x$.