How to Solve a Statics Truss Problem at Joint C Using the Joint Method?

[bergausstein]

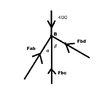
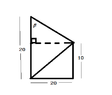
can you help me continue this problem. I'm stuck @ joint C. please use joint method.
please click the image to fully view it. thanks!
View attachment 1870

 

[BAdhi]

Re: statics truss problem.

When trying to solve these kind of problems try to find the stress of the nodes where there are only two unknown forces (since you can only get two equations per node). You've chosen the node A first, which is fine since $F_{AX}$ is zero thus leaving with only two unknown stresses.

But if you chose node C next you will find there are three unknowns. So my advice is analyse the Node B (which has only two unknown stresses) before going for node C. From there you can find the stress of the joint $F_{BC}$.

Now you'll only have two unknowns in node C since $F_{AC}$ and $F_{BC}$ is known.

 

[bergausstein]

Re: statics truss problem.

can you help me create the free body diagram at joint B. thanks!

 

[BAdhi]

View attachment 1876

$$\begin{align}
\rightarrow \displaystyle \Sigma \vec F &= 0\\
F_{AB} \sin \alpha - F_{BD}\sin{\beta} &= 0
\end{align}$$

$$\begin{align}
\uparrow \displaystyle \Sigma \vec F &= 0\\
F_{AB} \cos \alpha + F_{BD}\cos{\beta} +F_{BC} -400&= 0
\end{align}$$

I think you can find the appropriate values for $\alpha$ and $\beta$. $F_{AB}$ is known from node A (please consider that I've taken stress of the arm AB as a compression while you've taken it as a tension).

 

[bergausstein]

I did find the angle $\alpha$ but I don't know how to find angle $\beta$. can you help me find it.

 

[BAdhi]

View attachment 1889

Use the right angle triangle.

 

[bergausstein]

$\beta=$63.4 degrees am I correct?

 

[BAdhi]

Yes that's correct. I hope you can manage to find the other stresses.

 

[paulmdrdo1]

how can we solve this using method of sections?