How to Solve a Trigonometry Word Problem Involving Distances

[nmnna]

Homework Statement

A map shows a straight road crossing two contour levels 100ft., 200ft. at P, Q. The length of PQ is 1.2 inches, and the scale of the map is 4 inches to the mile. What average angle does the road make with the horizontal?

Relevant Equations

$$\tan(\alpha) = \frac{opposite \ side}{adjacent \ side}$$

The sketch:

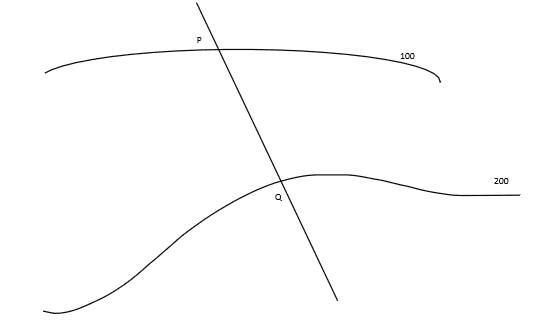
First of all find the length of PQ on i.e
$$4 \ inches - 1 \ mile$$
$$1.2 \ inches - x \ mile$$
$$x = \frac{1.2}{4} = 0.3 \ mile = 1584 \ ft$$

Now, I do not understand where shall I draw the horizontal, and the connection between the lengths of the contours, so I'll be grateful if you give me some hints for solving this problem.
Thank you.

 

[PeroK]

Why don't you draw the road incline from the side?

 

[nmnna]

Why don't you draw the road incline from the side?

Like this?

 

[PeroK]

No. From the side. So you can see the road going uphill!

 

[nmnna]

No. From the side. So you can see the road going uphill!

You mean from the opposite side? Sorry for my dumbness..

 

[PeroK]

A map is a "Plan". You want an "End Elevation" or "Side Elevation":

 

[nmnna]

A map is a "Plan". You want an "End Elevation" or "Side Elevation":

I think I understand now.
So the difference between the heights of the road is 100, I have the length of PQ, what I need to do now is to calculate the angle, right?

 

[PeroK]

I think I understand now.
So the difference between the heights of the road is 100, I have the length of PQ, what I need to do now is to calculate the angle, right?

Note that the distances on a map (you should be able to find out this sort of thing yourself from the Internet) are horizontal distances, not the hypoteneuse of slopes.

 

[nmnna]

Note that the distances on a map (you should be able to find out this sort of thing yourself from the Internet) are horizontal distances, not the hypoteneuse of slopes.

Okey, sorry for the trouble