How to solve for the magnitude and angle in this situation?

[Vanessa Avila]

Homework Statement

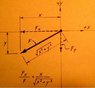
Each one of the force vectors are surrounded with dimensions. But you're not given any angles. How do you solve for the resultant vector like that?

Homework Equations

Fr = F1 + F2 + F3

The Attempt at a Solution

I tried taking the arctan(200/210) on the 435 N vector to get the angle for that but I don't think that's right.

 

[TomHart]

What did you get for the arctan (200/210)? And what angle would that represent?

 

[Vanessa Avila]

What did you get for the arctan (200/210)? And what angle would that represent?

I got 43.6 degrees. Would that be the angle between 435 N and the positive x-axis?

 

[Vanessa Avila]

What did you get for the arctan (200/210)? And what angle would that represent?

Or would that be the entire angle between positive x and y axis?

 

[TomHart]

If all of those numbers represent relative size of the vector, then yes, it looks like you got it right the first time - that 43.6 degrees is the angle between the 435 N vector and the positive x-axis. It's kind of a strange problem, but you are on the right track if you continue with what you are doing. It was a little confusing on the upward left pointing vector. Are the dimensions of that vector 70 and 210?

 

[Vanessa Avila]

If all of those numbers represent relative size of the vector, then yes, it looks like you got it right the first time - that 43.6 degrees is the angle between the 435 N vector and the positive x-axis. It's kind of a strange problem, but you are on the right track if you continue with what you are doing. It was a little confusing on the upward left pointing vector. Are the dimensions of that vector 70 and 210?

Oops i messed up on my drawing. The one on the left is 240 and the blue line on the top should be 70. Sorry about that!

 

[David Lewis]

Are the dimensions of that vector 70 and 210?

No. From the Pythagorean Theorem it appears the magnitude of the vector, and the x and y dimensions are to a different scale or denominated in different units.

In any case the first step is to resolve each vector into its x and y components. You can calculate the hypotenuse of the right triangle formed by the x and y dimensions, and then use proportional parts of similar triangles to find the x and y components for each vector.

 

[TomHart]

Oops i messed up on my drawing. The one on the left is 240 and the blue line on the top should be 70. Sorry about that!

No, I just read it wrong. You were right. It was 70 and 240. It just looked a little confusing the way it was shown.

 

[Tom.G]

You have all the X and Y components of each vector. Are you sure you need the individual angles?

 

[David Lewis]

Good point. It's usually easier in this situation to take advantage of the fact that corresponding sides of similar triangles are all in the same proportion.

 

[David Lewis]

The vectors' lines of action are defined by Cartesian coordinates (you can think of the x and y dimensions as position vectors). So by similar triangles we know the magnitude of the x component of the vector divided by the magnitude of the vector equals the x dimension divided by the distance from the origin to the vector's head.

 

[Vanessa Avila]

The vectors' lines of action are defined by Cartesian coordinates (you can think of the x and y dimensions as position vectors). So by similar triangles we know the magnitude of the x component of the vector divided by the magnitude of the vector equals the x dimension divided by the distance from the origin to the vector's head.

so by doing that for each force vector, I'll be able to get the value for the resultant?

 

[David Lewis]

Yes indeed. Just add the x force components together, and then the y force components together, as if they were scalars. Those algebraic sums will equal the x and y components of the resultant. Keep in mind the left and down directional senses are assigned a negative sign.

 

[Vanessa Avila]

Yes indeed. Just add the x force components together, and then the y force components together, as if they were scalars. Those algebraic sums will equal the x and y components of the resultant. Keep in mind the left and down directional senses are assigned a negative sign.

Awesome. Thanks a lot!