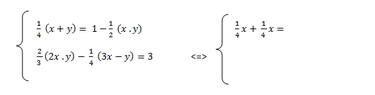- #1
AstroBoy1
- 1
- 0
Can someone solve this, i know its not very hard but for me it is :/
View attachment 2014
The dot . is meaned to be * (multiplication)
can someone help me :)
View attachment 2014
The dot . is meaned to be * (multiplication)
can someone help me :)
Attachments
Last edited by a moderator: