How to solve spring mass damper system manually?

[k.udhay]

TL;DR

Is it possible to solve a spring mass damper system manually? Pl. show some examples?

The other day when I solved a spring mass damper system in Matlab, I was curious how in olden days would have people solved the equation. We all know the 2nd order differential equation of the system:

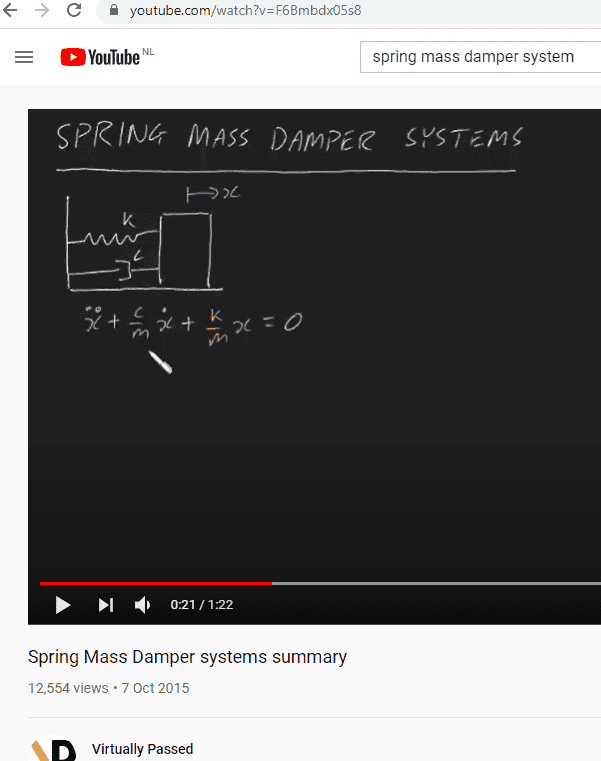
However if I know the time, damping coefficient, stiffness and mass, will I be able to find 'x' manually? Are there some examples? I referred to my old engineering engineering textbook and failed to find a suitable example.

 

[BvU]

Hi,

The way you found it on utube is the same way you can find the damped oscillator ! Once you've read all that, the solution isn't far away !

 

[BvU]

Summary:: Is it possible to solve a spring mass damper system manually? Pl. show some examples?

I referred to my old engineering engineering textbook and failed to find a suitable example

Must be a pretty advanced textbook

The general way to solve such a thing is to try solutions like $A\,e^{kx}$ and see what you need for $A$ and $k$ to satisfy the equation ...

 

[tech99]

If you take the electrical analogues of mass (inductance), spring compliance (capacitance), the electrical formulas are very easy. Damping coefficient can be converted to resistance. I notice old textbooks recommending conversion to electrical parameters for solving complex problems such as resonance, filters etc.

 

[anorlunda]

If you take the electrical analogues of mass (inductance), spring compliance (capacitance), the electrical formulas are very easy. Damping coefficient can be converted to resistance. I notice old textbooks recommending conversion to electrical parameters for solving complex problems such as resonance, filters etc.

Indeed yes. That's what gave birth to analog computers. In their day, they were very useful and fun too.

 

[k.udhay]

Must be a pretty advanced textbook

The general way to solve such a thing is to try solutions like $A\,e^{kx}$ and see what you need for $A$ and $k$ to satisfy the equation ...

Thanks BvU. I referred to the "solution" page you recommended where they start solving the differential equation assuming the solution is of the form "x = Ce^(λt)". So if this equation directly gives a simple solution for the position of mass x, the 2nd order differential equation that includes mass, stiffness etc. becomes redundant, right? We only solve "x = Ce^(λt)" and find x and other derivatives. Why did we write a governing equation at all?

 

[k.udhay]

If you take the electrical analogues of mass (inductance), spring compliance (capacitance), the electrical formulas are very easy. Damping coefficient can be converted to resistance. I notice old textbooks recommending conversion to electrical parameters for solving complex problems such as resonance, filters etc.

Despite of the fact that I am completely out of touch with electrical engineering, I will try to understand as much as I can. Thanks a lot for suggesting me a good analogy.

 

[hutchphd]

Here is the chapter from Sears et al,
https://opentextbc.ca/universityphysicsv1openstax/chapter/15-5-damped-oscillations/

 

[BvU]

I referred to the "solution" page
...
Why did we write a governing equation at all?

Do you mean 'characteristic equation' ? The word 'governing' does not occur there ...

 

[k.udhay]

Do you mean 'characteristic equation' ? The word 'governing' does not occur there ...

Sorry my bad. Yeah the characteristic equation. Once we know it is a second order differential equation, is it no longer needed? Can we describe the whole system with the assumed solution "x = Ce^(λt)"?

 

[BvU]

No. At a minimum it would be $C_1 e^{λ_1t} + C_2 e^{λ_2t}$ but we still have to investigate if the $C$ and $\lambda$ exist, and -- if so -- how many (cf critical damping case). And they have to be linked to the parameters and the initial conditions.

 

[BvU]

Re:

my old engineering textbook

In the curriculum for engineers there should also be math lectures, prefereably given by mathematicians. And second order differential equations should be on the menu.

 

[k.udhay]

Re:
In the curriculum for engineers there should also be math lectures, prefereably given by mathematicians. And second order differential equations should be on the menu.

I was a poor student in math and I am paying for it now :|

 

[BvU]

Maybe you can afford it better to pay now ?

 

[Dr.D]

Re:
In the curriculum for engineers there should also be math lectures, prefereably given by mathematicians. And second order differential equations should be on the menu.

There are pros and cons to having math faculty teach differential equations.

The first time I took DE, I took it in the "pure math" department at my university. We spent all semester proving properties of the solution of x''+K^2 x = 0, but we never solved the equation. I thought that was pretty worthless, so I took the course again in the "applied math" department. There, we had a doctoral student who talked all semester about his research involving the Wronskian, again pretty pointless. After that, I learned how to solve the differential equation in ME and EE courses.

 

[anorlunda]

The first time I took DE, I took it in the "pure math" department at my university.

I went to a 4 year engineering college, far from any city, frigid climate, no math department, no females. That style of college is very outdated today, but it had some advantages.

 

[Dr.D]

I went to a 4 year engineering college, far from any city, frigid climate, no math department, no females. That style of college is very outdated today, but it had some advantages.

What works well should never be out of date. In my case, the problem was not the females, but rather the faculty.