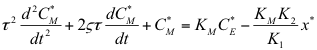MHB How to Solve This 2nd Order ODE in Control Systems?

ChemEng2
Messages
1
Reaction score
0
I'm trying to solve this equation analytically, but I can't even find the auxiliary equation or general solution!

View attachment 1867

Km = 0.5
C*e = 0
K2 = 0.03
K1 = 0.05
x* = 49
 

Attachments

  • wGsp94E.png
    wGsp94E.png
    1.6 KB · Views: 102
Physics news on Phys.org
What is $\tau$ and what is $\zeta$? If they do not depend on $t$, then this equation is fairly straight-forward (just assume $C_{m}=e^{kt}$, plug in, and solve for $k$, followed by finding a particular solution of the form $C_{m}=A$.)
 
I'd also advise substituting the values for your parameters, the equation will be much easier to read at least...
 
Thread 'Direction Fields and Isoclines'

Thread 'Direction Fields and Isoclines'

I sketched the isoclines for $$ m=-1,0,1,2 $$. Since both $$ \frac{dy}{dx} $$ and $$ D_{y} \frac{dy}{dx} $$ are continuous on the square region R defined by $$ -4\leq x \leq 4, -4 \leq y \leq 4 $$ the existence and uniqueness theorem guarantees that if we pick a point in the interior that lies on an isocline there will be a unique differentiable function (solution) passing through that point. I understand that a solution exists but I unsure how to actually sketch it. For example, consider a...
View full post »

Similar threads

I Fundamental matrix of a second order 2x2 system of ODEs
Replies
2
Views
4K
A Seeking advice about solving an ODE
Replies
3
Views
3K
I Trying to obtain a 2nd order ODE
Replies
6
Views
2K
MHB -a.3.2.96 Convert a 2nd order homogeneous ODE into a system of first order ODEs
Replies
8
Views
6K
I 2nd order ODE numerical solution
Replies
9
Views
3K
Existence of general solution, 2nd order ODE
Replies
14
Views
2K
MHB How Do I Solve this 2nd Order Non-Linear ODE and Find Its Equilibrium Points?
Replies
3
Views
3K
I Question about solving linear first order non-homogeneous ODEs
Replies
3
Views
3K
A Variation of Parameters for System of 1st order ODE
Replies
1
Views
2K
Why does the 2nd order homogeneous linear ODE have 2 general solutions?
Replies
1
Views
2K

Hot Threads

Recent Insights

Back
Top