- #1
Tapias5000
- 46
- 10
- Homework Statement
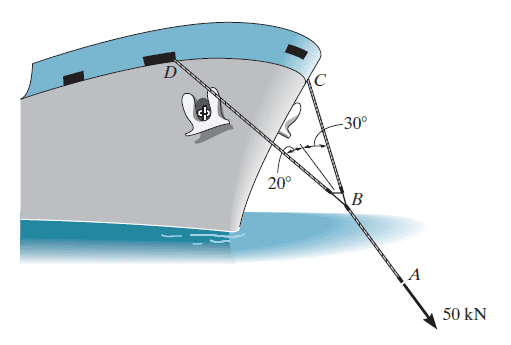
- The towing pendant AB is subjected to the force of 50 kN exerted by a tugboat. Determine the force in each of the bridles, BC and BD, if the ship is moving forward with constant velocity.
- Relevant Equations
- Σfx=0 and Σfy=0
This is the image of the problem
I tried to solve it and I got the following is it correct?
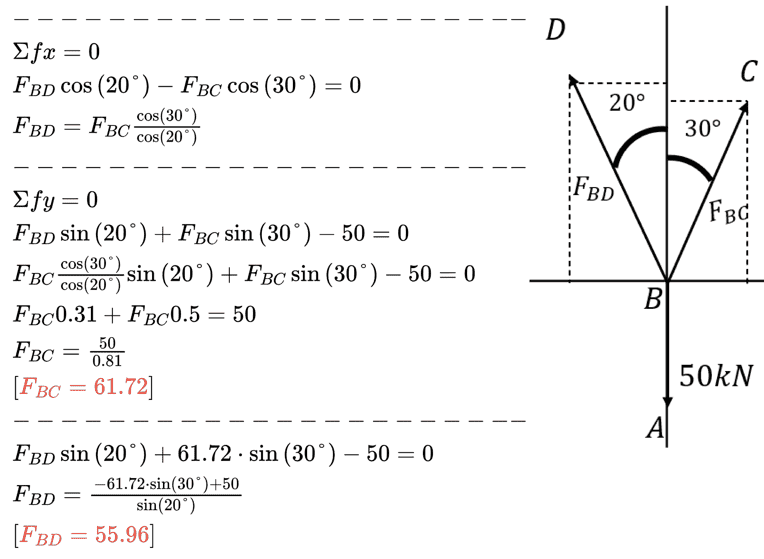
I tried to solve it and I got the following is it correct?