Oleksii
- 6
- 0
- Homework Statement
- .
- Relevant Equations
- .
Hi. I have next task:
Three current sources with EMF E1 = 11 V, E2 = 4 V and E3 = 6 V and three resistors with
resistance R1 = 5 Ohms, R2 = 10 Ohms and R3 = 2 Ohms are connected, as shown on picture below.
Determine the current strengths I in the resistors. Internal resistance sources neglect.
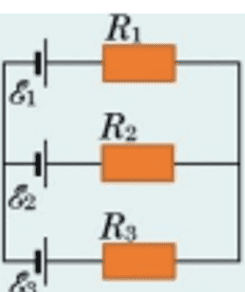
How to solve this using Kirchhoff's laws? I understand that we have to make a system of 3 equations (because we have 3 variables), but the crux of the problem is that I don't know how to set them.
My attempt:
E1 - E2 = I1R1 - I2R2
E2 - E3 = I2R2 - I3R3
E1 - E2 - E3 = I1R1 - I2R2 - I3R3
Solve of this system:
I1 =11/5A
I2 = 2/5A
I3 = 3A
I took 12, 23, and 123 circles. But this answer is impossible because at least one of the currents has to be geative.
Three current sources with EMF E1 = 11 V, E2 = 4 V and E3 = 6 V and three resistors with
resistance R1 = 5 Ohms, R2 = 10 Ohms and R3 = 2 Ohms are connected, as shown on picture below.
Determine the current strengths I in the resistors. Internal resistance sources neglect.
How to solve this using Kirchhoff's laws? I understand that we have to make a system of 3 equations (because we have 3 variables), but the crux of the problem is that I don't know how to set them.
My attempt:
E1 - E2 = I1R1 - I2R2
E2 - E3 = I2R2 - I3R3
E1 - E2 - E3 = I1R1 - I2R2 - I3R3
Solve of this system:
I1 =11/5A
I2 = 2/5A
I3 = 3A
I took 12, 23, and 123 circles. But this answer is impossible because at least one of the currents has to be geative.
Last edited: