- #1
Benjamin_harsh
- 211
- 5
- Homework Statement
- A and B leave their places and start moving towards each other. If they are 50m apart after both 2 min and 3 mins, how far are their places?
- Relevant Equations
- So, at 2 minutes - distance traveled by A = 2x and similarly by B = 2y
A and B leave their places and start moving towards each other. If they are 50m apart after both 2 min and 3 mins, how far are their places?
I can able to draw a diagram for this problem:
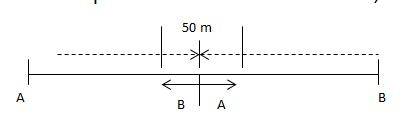 Take distance between their places as D
Take distance between their places as D
Speed of A = x meter /minutes
Speed of B = y meter/minutes
So, at 2 minutes - distance traveled by A = 2x and similarly by B = 2y
From here, how to proceed?
I can able to draw a diagram for this problem:
Speed of A = x meter /minutes
Speed of B = y meter/minutes
So, at 2 minutes - distance traveled by A = 2x and similarly by B = 2y
From here, how to proceed?