How to take a moment into account for deflection of a beam

[Mech_LS24]

Homework Statement

I have to calculate the deflection at the end of a beam due to a force. How do I find the moments in a beam while their are only forces applied (with pivots/hinges).

Relevant Equations

Sigma_bending = F*L^3 / 3EI
Theta = M*L / 3EI

Hello!

I have to calculate the deflection of a beam at at given point (C). The books says the should be a moment which plays a role in this deflection. How does this moment occur? I have drawn a FBD but couldn't find a moment? Should I divided the beam into separate parts or so? What am I missing here?

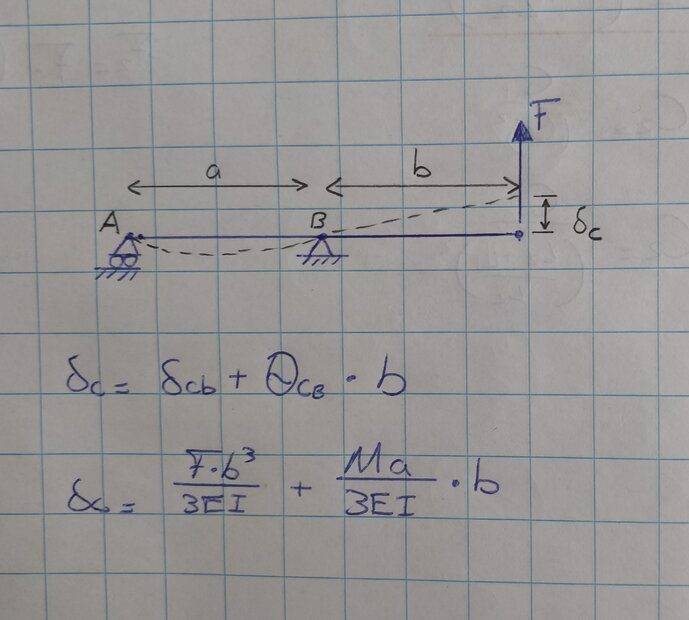
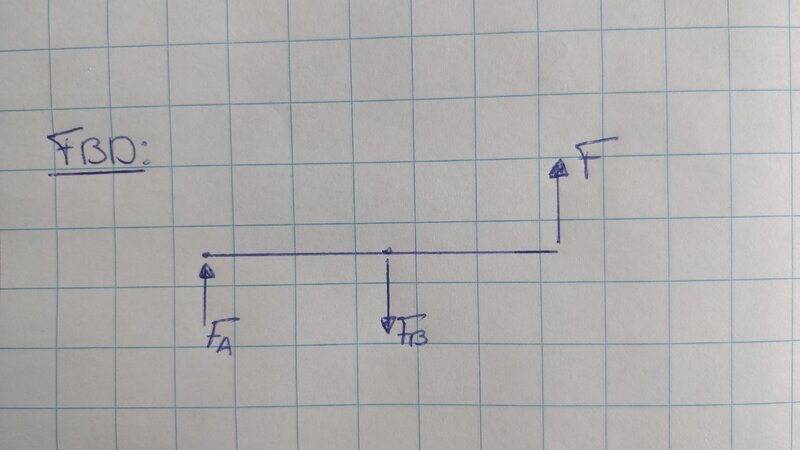
Thanks!

 

[Lnewqban]

Did you do a balance of moments?
If you have F and b, you have at least one moment.

If that beam is smiling or bending, a moment is compressing the top fibers of it and stretching the bottom fibers.

Please, see:
https://en.m.wikipedia.org/wiki/Bending

https://www.engineeringtoolbox.com/cantilever-beams-d_1848.html

https://www.engineeringtoolbox.com/beam-stress-deflection-d_1312.html
:)

 

[Mech_LS24]

Did you do a balance of moments?
If you have F and b, you have at least one moment.

If that beam is smiling or bending, a moment is compressing the top fibers of it and stretching the bottom fibers.

Please, see:
https://en.m.wikipedia.org/wiki/Bending

https://www.engineeringtoolbox.com/cantilever-beams-d_1848.html

https://www.engineeringtoolbox.com/beam-stress-deflection-d_1312.html
:)

Thanks,

What do you exactly mean with balance of moments? I think I know what you mean but then there should be another moment due to the Fa force (Fa*a = Moment)?

I can't see their is a moment because the beam isn't clamped, it is only supported by rollers and a pivot? Bit confused here...

The book also stated that we can move the force F at the position of pivot B. They actually separate the beam with moving force F on pivot B and add that moment. How is that possible?

 

[haruspex]

You have not shown any weight of the beam. Show it as a distributed load. If it is massless it won't bend. It won't even stay on the supports!

Edit: I believe I misread the diagram. The solid circles at the tops of the pivots are so small I did not see them, so read them as unpinned.

 

[Lnewqban]

Thanks,

What do you exactly mean with balance of moments? I think I know what you mean but then there should be another moment due to the Fa force (Fa*a = Moment)?

I can't see their is a moment because the beam isn't clamped, it is only supported by rollers and a pivot? Bit confused here...

The book also stated that we can move the force F at the position of pivot B. They actually separate the beam with moving force F on pivot B and add that moment. How is that possible?

You are welcome.

According to Newton's second law, if the beam is not moving in any direction, or rotating about any point in space, the summations of all the forces and all the moments (if any) acting on it must both equal zero.

As represented, that roller allows horizontal movement and rotation only, and restricts any vertical movement.
That pivot allows rotation only and restricts any horizontal and vertical movement.

If the distance b becomes zero and the force F becomes colinear with the reaction force Ry at pivot B, the lever of force F disappears, as well as its capability to induce any moment in that system.
The book may explain that the moment created by force F and lever b, can be represented by a punctual moment at pivot B, or anywhere else along the beam.
The magnitude of that punctual moment will still be F x b.
Could you show us a link or picture of the book's problem?

 

[Mech_LS24]

As represented, that roller allows horizontal movement and rotation only, and restricts any vertical movement.
That pivot allows rotation only and restricts any horizontal and vertical movement.

I can follow along here.

But still struggling why that force at pivot B is there, you say if the distance b becomes zero, the force becomes colinear with the reaction force Ry at pivot B. What do you mean with colinear? If the distance B becomes 0, there isn't a force at all on the beam??

A picture, but I have simplified it a bit in the first post because I only didn't get that figure 12.29c:

 

[Lnewqban]

Please, note that the directions of the force applied on point C are opposite in your diagram of the first post and in the book's picture; that changes things.

It seems that the book tries to explain that the situation pictured in (a) is equivalent to the superposition of the situations pictured in (b), (c) and (d).

What I meant by colinear was that, as represented in situation (c), there is no distance between the lines of applications of the forces F and reaction force at B; therefore, there is no moment induced by F or Ryc at pivot C, and an imaginary suplemental moment has needed to be introduced in order to keep the beam bent as in situation (a).

There are several methods to calculate the deformation of a beam under bending loads.
It seems that those pictures from your book are explaining one of them: the "Superposition method".

Please see method 5 and related typical problems in this link:
https://mathalino.com/reviewer/mechanics-and-strength-of-materials/chapter-6-beam-deflections

Once you get the concept, we could draw a diagram of forces and moments together.

 

[Lnewqban]

The attached diagram copied from the website of the above link explains it better than I could.

The deflection of the beam for the length between the supports is going to be the same for either case.

That deflection, regarding maximum value and shape adopted by the beam (see red line) within that lenght, is different from the natural deflection that would be adopted by the beam under the distributed load alone.

The reason is that either the shown concentrated force or the shown punctual moment are helping that length to deform less.

 

[Mech_LS24]

What I meant by colinear was that, as represented in situation (c), there is no distance between the lines of applications of the forces F and reaction force at B; therefore, there is no moment induced by F or Ryc at pivot C, and an imaginary suplemental moment has needed to be introduced in order to keep the beam bent as in situation (a).

There is a distance between the F and reaction force in B, 2 meters? Ryc is a virtual reaction force at C? We have actually two deflections in point C as shown in the pictures (c) and (d), Vc2 and Vc3. But Vc2 is already the total deflection of point C isn't it? Sorry my English isn't very decent, maybe that's why I can't follow you, excuse me for that.

I thought I was quite familiar with the "superposition method", but that was for beam without an overhang. Looks like it is a bit more complicated..

The attached diagram copied from the website of the above link explains it better than I could.

Looking into it right now :)

Once you get the concept, we could draw a diagram of forces and moments together.

Thanks!