- #1
Javier Mont
- 9
- 0
I understand for linear momentum the measure of the dificulty to take a body to the rest. But when I do the next exercises, I find that it requires less force for one body compared to the other with same linear momentum.
Can someone explain me what to understand in an intuitive way what to expect when I see a certain magnitud of linear momentum from a body?
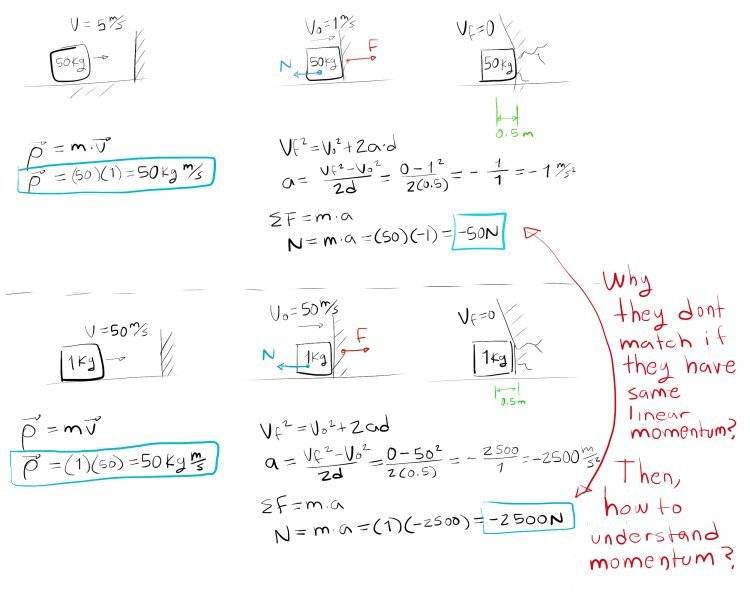
Can someone explain me what to understand in an intuitive way what to expect when I see a certain magnitud of linear momentum from a body?
Attachments
Last edited by a moderator:

