How to use the Double integration method for an overhanging beam?

[Guruprakash]

TL;DR Summary

Forming an equation for beam with point load at the end is well known. When we take a section at distance 'x' we ought to neglect the point load or reaction at end of the beam. But how the force influence is take into account in the equation? But when we form a equation for overhanging beam with point load which is offset from the end we include all the force and reaction in the equation.

In case of overhanging beam with point load at the end. For example:

(here RA-reaction is negative)

The equation will be as follows (by double integration method):

, as we can see the equation will not have Point load (10kN) term in it.

1) How the influence of the point load is accounted in this equation? Is it accounted by the reaction forces ([R][/A], [R][/B]) as it is calculated from the point load(10kN)?

In case of overhanging beam with offset point load from the end. For example:

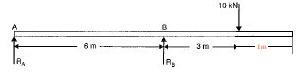
The equation is (for section at x=12)

.

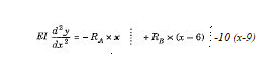2) Is the above equation is correct? If yes, it has all the terms of reactions and the point load and if we take a section from right to left there will be no reaction (RA) term in the equation.

Kindly explain me how double integration method equation works.

 

[PhanthomJay]

You don’t have to use double integration if you are just looking for bending moments in a statically determinate beam. The moments at any section along the beam are determined by the equilibrium equations. In particular, the sum of moments about any point on the beam must equal zero, and that includes summing moments about a load or support point.