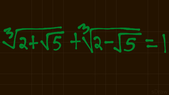mathdad
- 1,280
- 0
Verify that both sides of the radical equation agree without using a calculator. See picture. How can this be done algebraically?
View attachment 7967
View attachment 7967
How to Verify a Radical Equation Algebraically?
- Context:
- Thread starter mathdad
- Start date
-
- Tags
- Radical
Join the discussion
Ask a follow-up here, or get your own question answered by working scientists, mathematicians and engineers — people, not an autocomplete.
Real named experts · corrections over time · the nuance an AI answer skips
2 replies · 2K views
Mathematics news on Phys.org
MarkFL
Gold Member
MHB
- 13,284
- 12
You asked this question before:
https://mathhelpboards.com/pre-calculus-21/radical-equation-2-a-23551.html
https://mathhelpboards.com/pre-calculus-21/radical-equation-2-a-23551.html
mathdad
- 1,280
- 0
It's good to know that this site keeps a record of posted questions as reference notes.
Similar threads
- mathdad
- · Replies 2 ·
- General Math
- Replies
- 2
- mathdad
- · Replies 10 ·
- General Math
- Replies
- 10
- mathdad
- · Replies 4 ·
- General Math
- Replies
- 4
- mathdad
- · Replies 2 ·
- General Math
- Replies
- 2
- mathdad
- · Replies 5 ·
- General Math
- Replies
- 5
- Mr Davis 97
- · Replies 2 ·
- General Math
- Replies
- 2
- Demystifier
- · Replies 6 ·
- Linear and Abstract Algebra
- Replies
- 6
- blackfriars
- · Replies 12 ·
- General Math
- Replies
- 12
- mathdad
- · Replies 10 ·
- General Math
- Replies
- 10
- mark2142
- · Replies 8 ·
- Precalculus Mathematics Homework Help
- Replies
- 8