- #1
scherz0
- 10
- 2
Here I'm asking solely about the circle pictograms. Please eschew referring to, or using, numbers as much as possible. Please explain using solely the circle pictograms. Undeniably, I'm NOT asking about how to divide numbers.
I don't understand
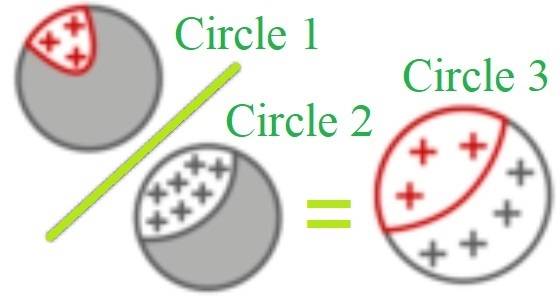
1. How do I "visually" divide Circle 1 (representing ##P(+ \cap D)##) by Circle 2 (##P(+)##) into Circle 3 (##P(+)##)?
2. I see that the bottom gray areas in Circles 1 and 3 disappear, but how does this pictorialize division?
I first precis the problem statement and percentages. Abbreviate Disease to D, positive test result to +. 1. The website postulates P(D) = 20%, P(+|D) = 90%, P(+|D^C) = 30%. What fraction of patients who tested positive are diseased?
"the proof above" refers to the Odds form of Bayes's Rule. For clarity, I replace the website's ##H_j## with ##D##, ##H_k## with ##D^C## and ##e_0## with ##+##.
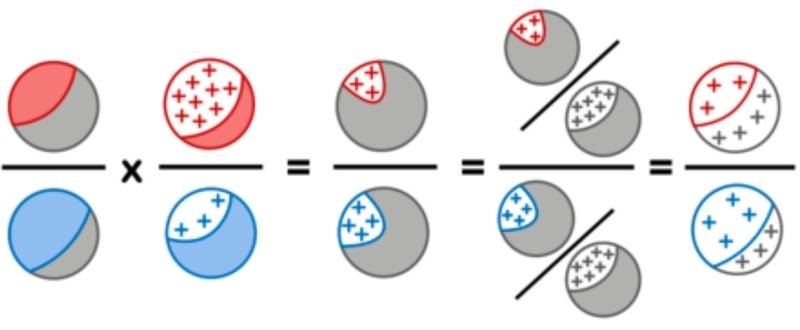
##\dfrac{P(D)}{P(D^C)} \times \dfrac{P(+|D)} {{P(+|D^C)}} = \dfrac{P(+ \cap D)}{P(+ \cap D^C)} = \dfrac{P(+ \cap D)/P(+)}{P(+ \cap D^C)/P(+)} = \dfrac{P(D|+)}{P(D^C|+)}##
I don't understand
1. How do I "visually" divide Circle 1 (representing ##P(+ \cap D)##) by Circle 2 (##P(+)##) into Circle 3 (##P(+)##)?
2. I see that the bottom gray areas in Circles 1 and 3 disappear, but how does this pictorialize division?
I first precis the problem statement and percentages. Abbreviate Disease to D, positive test result to +. 1. The website postulates P(D) = 20%, P(+|D) = 90%, P(+|D^C) = 30%. What fraction of patients who tested positive are diseased?
3/7 or 43%, quickly obtainable as follows: In the screened population, there's 1 sick patient for 4 healthy patients. Sick patients are 3 times more likely to turn the tongue depressor black than healthy patients. $(1:4)⋅(3:1)=(3:4)$ or 3 sick patients to 4 healthy patients among those that turn the tongue depressor black, corresponding to a probability of 3/7=43% that the patient is sick.
Using red for sick, blue for healthy, grey for a mix of sick and healthy patients, and + signs for positive test results, the proof above can be visualized as follows:
"the proof above" refers to the Odds form of Bayes's Rule. For clarity, I replace the website's ##H_j## with ##D##, ##H_k## with ##D^C## and ##e_0## with ##+##.
##\dfrac{P(D)}{P(D^C)} \times \dfrac{P(+|D)} {{P(+|D^C)}} = \dfrac{P(+ \cap D)}{P(+ \cap D^C)} = \dfrac{P(+ \cap D)/P(+)}{P(+ \cap D^C)/P(+)} = \dfrac{P(D|+)}{P(D^C|+)}##
Last edited by a moderator: