- #1
JimJCW
Gold Member
- 208
- 40
The following figure shows observed distance modulus (µ) vs. redshift (z) data (references of data sources are available):
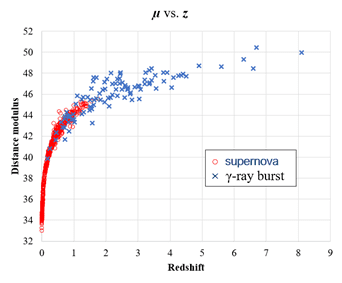
How well do cosmological models, such as ΛCDM and models based on non-expanding universe, explain these observed data?
For explanation of terms, please see,
How well do cosmological models, such as ΛCDM and models based on non-expanding universe, explain these observed data?
For explanation of terms, please see,