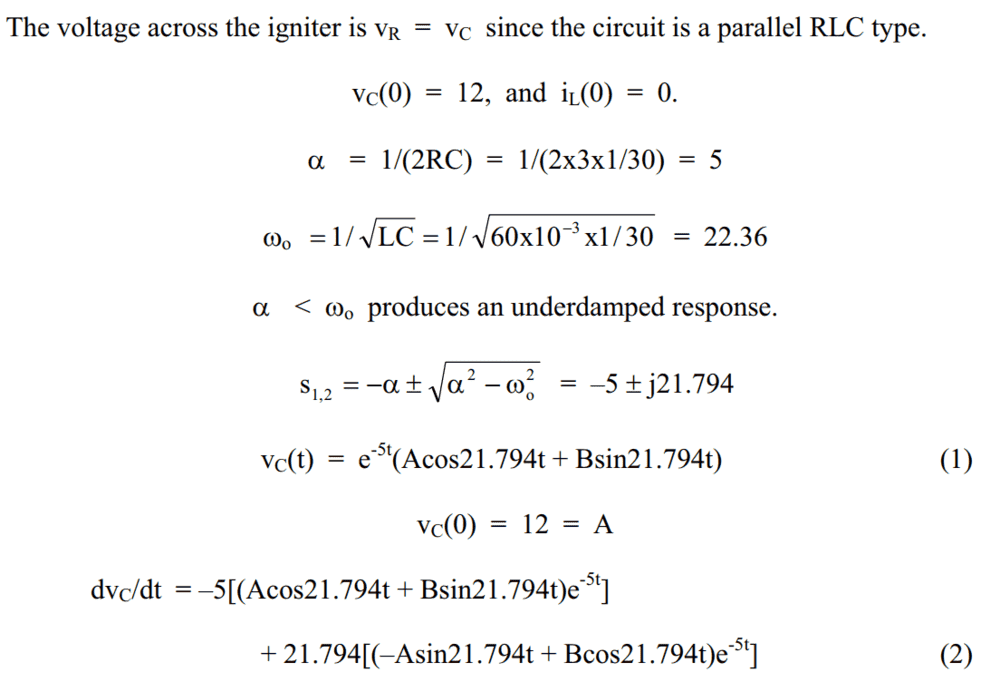How were tangent terms derived in solving for eqn (2) in a second-order circuit?

  • Topic: Engineering 
  • Thread starter Thread starter paulmdrdo
  • Start date Start date
  • Tags Tags
    Circuit General
Join the discussion
Registration is free. Start your own thread to ask a follow-up.
Sign up Log in
1 reply · 2K views
paulmdrdo
Messages
89
Reaction score
2
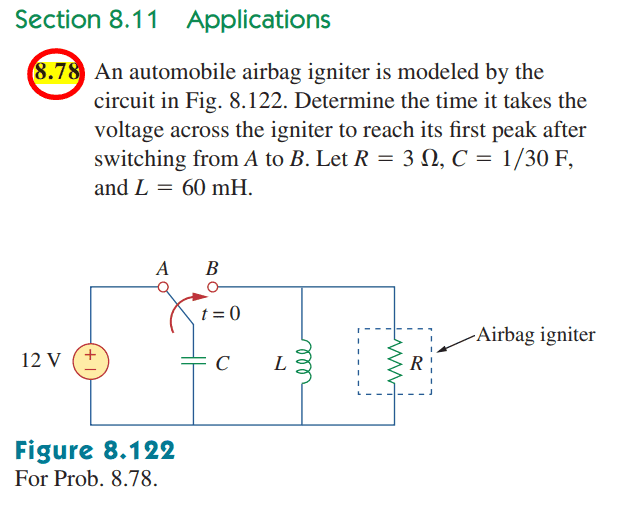
Homework Statement
Find the expression for ##v(t)##
Relevant Equations
SEE ATTACHED PHOTO
I was trying to follow the solution for this problem and got stuck in the last portion of the solution. I encircled the part that I did not understand. I can't figure out how the solver was able to come up with tangent terms. Please enlighten me. TIA
242126
242127
242128
 
Physics news on Phys.org

Discussion

The author equated eqn (2) to 0
then extracted (and divided both sides by) the common factor 5(cos 21.749t)
 

Similar threads

Engineering Solving a Second Order Circuit for Capacitor Voltage

  • Vishera
  • · Replies 4 ·
  • Engineering and Comp Sci Homework Help
Replies
4

Engineering Determining Constants in Second Order Circuit Analysis

  • shniflbaag
  • · Replies 1 ·
  • Engineering and Comp Sci Homework Help
Replies
1

Engineering Solving a second order circuit with phasors

  • Evales
  • · Replies 16 ·
  • Engineering and Comp Sci Homework Help
Replies
16

Engineering Deriving Second Order Circuit Equation Using Natural Response

  • p75213
  • · Replies 4 ·
  • Engineering and Comp Sci Homework Help
Replies
4

Engineering General second order circuit problem - Find V(t) for t > 0

  • VinnyCee
  • · Replies 9 ·
  • Engineering and Comp Sci Homework Help
Replies
9

Second order circuit with two resistors, inductors and current source

  • VinnyCee
  • · Replies 17 ·
  • Introductory Physics Homework Help
Replies
17