Huygen's Principle doesn't necessarily imply the law of reflection

[etotheipi]

There are many diagrams like the following

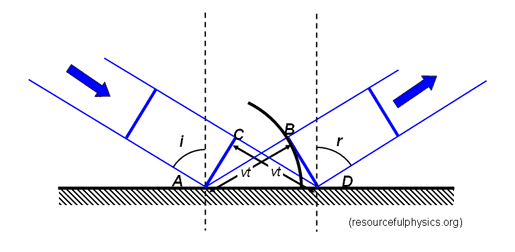
which demonstrate that if A acts as a point source of wavelets, then we will have constructive interference in the case that $i=r$ as shown, as we can show with a little geometry that the path difference is zero.

However, surely this isn't the only option, since we can let the path difference between the two waves shown equal any multiple of $\lambda$ a consequently obtain many different orders. If we accept Huygens principle and apply it to a smooth reflector, we should obtain reflection across many different angles.

So why is it that only the zeroth order is included in the law of reflection?

Previously, I thought that we could only get the "scattering" required with a reflective diffraction grating, however Huygen's principle seems to imply that the diffraction grating principle is correct even for a smooth plane mirror - is this right?

 

[tech99]

If we had just two rays, on the extremities of the incident beam, they would induce current in two places (like dipoles) on the reflector surface and give rise to multiple re-radiated lobes, in the manner of Young's Slits. But the incident beam is solid, so across the surface of the reflector we have a row of points which will re-radiate. The phasing of these is such as to create a parallel reflected beam in the direction i = r. The radiation in other directions tends to average to zero.
Notice, incidentally, that one cannot have a parallel beam with finite diameter except close to a source.

 

[etotheipi]

But the incident beam is solid, so across the surface of the reflector we have a row of points which will re-radiate.

Thank you, I forgot to consider this.

If the incident angle is $i$ and the reflected is $r$, then for any two rays to interfere constructively we require $$d(\sin{i}-\sin{r})= n\lambda$$Now suppose two rays separated by a distance $d$ interfere constructively along their common first order, so that $d(\sin{i}-\sin{r}) = \lambda$. The ray in between them at a distance $\frac{d}{2}$ will be such that its path difference from the two previous rays is $$\frac{d}{2}(\sin{i}-\sin{r}) = \frac{\lambda}{2}$$ and we will get destructive interference.

So the result is the only maximum is where $i=r$. Is this right?

 

[Dale]

So why is it that only the zeroth order is included in the law of reflection?

Only the zeroth order works for all wavelengths. You can build reflectors called diffraction gratings that cause the higher order reflections you are describing. They do reflect at other angles, but are very sensitive to wavelength.

 

[sophiecentaur]

however Huygen's principle seems to imply that the diffraction grating principle is correct even for a smooth plane mirror - is this right?

Yes it is but, for a uniform reflector, the equivalent diffraction slits have zero spacing. The limit as the spacing goes to zero gives only the zeroth order beam. In any other direction the addition of all the Huygens sources gives zero.
Take any diffraction grating and see where the second order beam occurs. Then double the pitch of the grating lines and the second order beam will be greater (double, in fact, for a wide spaced grid). Repeat the process and the second order beam is deflected more. Carry on with that process and the second order beam will be deflected by more than the angle of the grating / mirror. So only the zeroth order beam will remain.

 

[tech99]

Yes, a diffraction grating is an underfilled array, so we have side lobes.

 

[sophiecentaur]

Yes, a diffraction grating is an underfilled array, so we have side lobes.

I just love it when people bring it all back to antenna theory.

 

[sophiecentaur]

I just love it when people bring it all back to antenna theory.

And on that theme, you have to remember that there will be a sin(x)/x distribution over the width of the reflected beam. You can't avoid that one.