Hydrostatics question - angled triangular gate?

[theBEAST]

Homework Statement

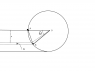
The question asks to find the magnitude of the pressure force on the gate:

The Attempt at a Solution

Here is the part of the solution:

I don't get why zc is 3.667m. Shouldn't it be 3 + (2/3)sin40 since you want the depth of the centroid from the surface to the gate?


Also, another way to solve this would be to find the horizontal force and vertical forces. This would mean that I would have to for the weight of the fluid under the gate in order to find the vertical force right?

 

[SteamKing]

If you draw the location of the centroid of the triangular gate on the diagram and work out the trigonometry, you will see that the location of the centroid in the problem statement is correct. Remember, the length of the gate from A to B is 2 / sin 50. You then draw 2/3 of this distance from B on the Front View. Working back from this point to the surface, you will see zc is 3.667 m.

 

[theBEAST]

If you draw the location of the centroid of the triangular gate on the diagram and work out the trigonometry, you will see that the location of the centroid in the problem statement is correct. Remember, the length of the gate from A to B is 2 / sin 50. You then draw 2/3 of this distance from B on the Front View. Working back from this point to the surface, you will see zc is 3.667 m.

Ah that makes a lot of sense, thank you.

So I decided to try the other method I mentioned where you take the magnitude of the Fhorizontal and Fvertical. However, my answer is off by around 3000N (the answer key gives 39000N). Do you guys know what is wrong?

 

[Sunil Simha]

Just check the vertical component of the hydrostatic-pressure force. I'm getting it near 25 kN.

 

[theBEAST]

Just check the vertical component of the hydrostatic-pressure force. I'm getting it near 25 kN.

Hmm... First off, am I right about the fact that there are only two vertical force - weight of the water and the projected vertical upwards force?

Also, I wasn't sure if I should include the weight of the gate in the vertical force calculations... Even if I did the answer isn't 25kN.

 

[Sunil Simha]

Hmm... First off, am I right about the fact that there are only two vertical force - weight of the water and the projected vertical upwards force?

Also, I wasn't sure if I should include the weight of the gate in the vertical force calculations... Even if I did the answer isn't 25kN.

Yes those are the only vertical forces.

Now excluding the weight, net force due to hydrostatic pressure*sin40 is the vertical component.

 

[theBEAST]

Yes those are the only vertical forces.

Now excluding the weight, net force due to hydrostatic pressure*sin40 is the vertical component.

Oh wow that is a very smart way to do it. So essentially you don't even solve for the vertical component, you wrote it in terms of the resultant force?

But in case I wanted to solve for it using the method I currently have written, how would I do it? Because if the gate was curve like a circle, your method will not work anymore right?

 

[Sunil Simha]

But in case I wanted to solve for it using the method I currently have written, how would I do it? Because if the gate was curve like a circle, your method will not work anymore right?

My method is valid for any shape as long as you can calculate the area because net force is equal to pressure times area of the surface and is perpendicular to the surface.

Could you please explain how you arrived at the vertical component as I did not follow what y_{bot} meant.

 

[theBEAST]

My method is valid for any shape as long as you can calculate the area because net force is equal to pressure times area of the surface and is perpendicular to the surface.

Could you please explain how you arrived at the vertical component as I did not follow what y_{bot} meant.

Right, but for a curved shape, you wouldn't know what the angle was so just finding the horizontal force would not be enough right? Because in this example, we know that the surface is flat so we can use Fvertical = Fresultant * sin40 for the vertical force and then

Fresultant² = Fhorizontal² + Fvertical²​

To solve for the resultant force.The method I used comes from a sample question in the textbook:

In the solution, for the part where they solve for the vertical force, we see that they take the pressure at the very bottom.

 

[theBEAST]

Does anyone know why this method does not work :O

 

[Sunil Simha]

Right, but for a curved shape, you wouldn't know what the angle was so just finding the horizontal force would not be enough right?

Thanks for showing me this method. I am seeing this for the first time. I usually employ integration to solve in case the gate is curved because that method can be used irrespective of the shape ( usually the integrals are solvable). I still don't get why they take the pressure at the bottom to find the vertical component of force though:( Could you please show how these formulae were derived or could you give a link to a site which shows the derivation?

 

[theBEAST]

Thanks for showing me this method. I am seeing this for the first time. I usually employ integration to solve in case the gate is curved because that method can be used irrespective of the shape ( usually the integrals are solvable). I still don't get why they take the pressure at the bottom to find the vertical component of force though:( Could you please show how these formulae were derived or could you give a link to a site which shows the derivation?

Unfortunately there is no derivation in the book.

As for the integration method, how can you use integration for the curved circular gate example from the textbook?

 

[Sunil Simha]

Check out the attachment for the diagram.

Now consider a small element of area along the lateral surface of the cylinder with subtends an angle dα at the center.

x=Rsinα
Pressure at this depth is ρg(h+x) and the force on the cylinder per unit length at this depth is simply the product of area = Rdα*unit length and is normal to the area i.e. directed to the center. It's x and y components can be found and separately integrated over required limits to get the total x and y components of force.

Though I cannot find any mistake in my argument, the integral misses the textbook's answer.
the X component that I get is ρgR(h+R/4) while the textbook says ρgR(h+R/2). There are similar discrepancies with the Y component. I shall check my integrals again tomorrow and tell you if I get anything.

 

[Saitama]

I am no expert. The y_component of force when calculated using integrals doesn't match the book's answer but x-component of force does.

The pressure at height h+Rsinα is P=ρg(h+Rsinα), the force acting on area dA is dF=PdA, where dA=Rdα. The direction of this force is radially towards the centre.
dF_x=dF\cos \alpha=ρg(h+Rsinα)R\cos \alpha d\alpha
Integrating the expression within the limits 0 to pi/2
F_x= ρgR\left(h+\frac{R}{2}\right)
which matches with the book's answer. However,
dF_y=dF\sin \alpha=ρg(h+Rsinα)R\sin \alpha d\alpha
F_y=ρgR\left(h+\frac{\pi R}{4}\right)

I would like an expert to comment on this.

 

[Sunil Simha]

Though I cannot find any mistake in my argument, the integral misses the textbook's answer.
the X component that I get is ρgR(h+R/4) while the textbook says ρgR(h+R/2). There are similar discrepancies with the Y component.

My bad. Thanks Pranav-Arora I rechecked my integrals. It matches with what you obtained.

 

[TSny]

I am no expert. The y_component of force when calculated using integrals doesn't match the book's answer but x-component of force does.

The pressure at height h+Rsinα is P=ρg(h+Rsinα), the force acting on area dA is dF=PdA, where dA=Rdα. The direction of this force is radially towards the centre.
dF_x=dF\cos \alpha=ρg(h+Rsinα)R\cos \alpha d\alpha
Integrating the expression within the limits 0 to pi/2
F_x= ρgR\left(h+\frac{R}{2}\right)
which matches with the book's answer. However,
dF_y=dF\sin \alpha=ρg(h+Rsinα)R\sin \alpha d\alpha
F_y=ρgR\left(h+\frac{\pi R}{4}\right)

I would like an expert to comment on this.

I'm no expert either, but your calculation looks correct to me. It agrees with the solution in the figure in post #9 where the vertical force on the cylinder would be $F_V = F_y - W$. Here, $F_y$ is the vertical force on the horizontal bottom surface of the volume of water below the cylinder as shown in the figure and $W$ is the weight of that water.

 

[Sunil Simha]

Thanks TSny,

According to our calculations, the vertical force due to the water would be 37.892 kN while the textbook says 39.2 kN. Though the difference is small, the answers still vary because of the methods used to obtain them.

So, my question is whether the textbook's method is an approximation. If so, how far is it valid or is there a limit after which the approximation fails?

 

[TSny]

I believe the 37.892 kN is the correct answer for the vertical force on the cylinder; whereas, the 39.2 kN is the correct answer for the vertical force on the horizontal bottom surface of the water that lies beneath the cylinder. The difference of these equals the weight of the volume of water that lies vertically beneath the cylinder.

 

[Sunil Simha]

I believe the 37.892 kN is the correct answer for the vertical force on the cylinder; whereas, the 39.2 kN is the correct answer for the vertical force on the horizontal bottom surface of the water that lies beneath the cylinder. The difference of these equals the weight of the volume of water that lies vertically beneath the cylinder.

I have a few doubts,

1. So are (referring to the diagram), F_v=37.892 kN and F_y=39.2 kN?
2.To find the weight per unit length of the cylinder, shouldn't F_v=37.892 kN be used as it is the vertical force component on the cylinder?

 

[TSny]

I have a few doubts,

1. So are (referring to the diagram), F_v=37.892 kN and F_y=39.2 kN?

Yes.

2.To find the weight per unit length of the cylinder, shouldn't F_v=37.892 kN be used as it is the vertical force component on the cylinder?

In going to part (b) where you want to find the weight per unit length of the cylinder, you should think of a free body diagram for the cylinder. Note that there will be horizontal and vertical components of "reaction" force at the hinge acting on the cylinder. These would have to be included in summing the forces in the horizontal and vertical directions. I think torque would be the way to go for this part.

 

[Sunil Simha]

Okay, so torque about the hinge is because of the vertical component of the normal reaction i.e. F_y and weight of the cylinder itself. Both act along the same distance from the hinge i.e. R(radius).

So when the water is just about to exit, the two should just balance each other and thus, F_y=mg
So 37892=m*9.81
or m= 4066 kg (per unit length of course)

Is this right?

 

[TSny]

Okay, so torque about the hinge is because of the vertical component of the normal reaction i.e. F_y and weight of the cylinder itself. Both act along the same distance from the hinge i.e. R(radius).

F_y does not have a moment arm equal to R. F_H also produces torque.

If you pick a small patch of area at a general location where the water contacts the cylinder, then the water will exert horizontal and vertical components of force on the cylinder as set up by Pranav-Arora. Both the horizontal and vertical components of force will produce torque about the hinge. The most direct way to get the net torque on the cylinder caused by the hydrostatic pressure is to integrate the torques due to these components of force.

[EDIT: Actually, I think it's easier to just integrate the magnitude dF of Pranav-Arora's force times the moment arm of the force, rather than finding the separate torques from dF_x and dF_y.]

 

[Sunil Simha]

Okay so, the figure I shall refer to in the following derivation is in the attachment.

So the force due to hydrostatic pressure at a depth (h+x) is
dF=ρg(h+Rsinθ)Rdθ(cosθi + sinθj)

And the radius vector from the hinge to that point is
r=R(1-cosθ)i-Rsinθj

So the differential torque is

dτ=r x dF

or dτ= R²ρg(Rsinθ + h)sinθ.dθ k

Hence net torque is τ = R²ρg(R∏/4 + h)k

Which is the same as the torque due to vertical component of the force acting at the center

 

[TSny]

Hence net torque is τ = R²ρg(R∏/4 + h)k

Which is the same as the torque due to vertical component of the force acting at the center

It's interesting that the answer can be interpreted that way. Is there a way to see that ahead of time or to see it intuitively?

 

[Sunil Simha]

It's interesting that the answer can be interpreted that way. Is there a way to see that ahead of time or to see it intuitively?

Well I don't know whether my reasoning is correct but I thought of it this way:

The net force acts along the radius and thus points to the center. Thus if I were to displace it along the same line such that it starts at the center, then the torque would be the simple cross product of the vectors.

 

[TSny]

The net force acts along the radius and thus points to the center. Thus if I were to displace it along the same line such that it starts at the center, then the torque would be the simple cross product of the vectors.

I don't follow what you are saying here. When you say "net force", are you referring to the net force dF that the water exerts on a small element of area of the cylinder?

 

[Sunil Simha]

I don't follow what you are saying here. When you say "net force", are you referring to the net force dF that the water exerts on a small element of area of the cylinder?

No, by net force I mean the total force on the cylinder due to hydrostatic pressure; the one that Pranav-Arora had calculated in post #14

 

[TSny]

No, by net force I mean the total force on the cylinder due to hydrostatic pressure; the one that Pranav-Arora had calculated in post #14

Then why can you say that this net force acts toward the center along the radius of the cylinder? At what point on the cylinder's surface are you taking this net force to act?

 

[Sunil Simha]

Then why can you say that this net force acts toward the center along the radius of the cylinder? At what point on the cylinder's surface are you taking this net force to act?

I thought because the force is normal to the surface area, it should act along the radius(normal to the surface). The point of action would be that, when joined to the center would make an angle of \theta=tan^{-1}|\frac{F_y}{F_x}| with the horizontal.

 

[TSny]

OK, good. It took me a while to see it. If you go back to the infinitesimal forces dF, each of these acts toward the center. So, you can slide each of these forces along the radius so they act at the center. And that would not change the torque of each dF about the axis of rotation. So, now all of the forces dF act at one point (the center). The total torque is equal to the torque due to the sum of these forces acting at the center. So, you can just take the net force to act at the center to find the net torque. That's pretty.

Thanks.