I calculating maximum gradient climbing ability of my car

[karabiner98k]

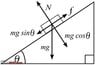
I want to calculate maximum gradient ability of my car in 1st gear to reach an estimation number.

The specification of the car is as follows:

Max torque = 155 nm @ 4250 RPM
Curb weight = 1200 kg
1st gear ratio = 3.454
Final Drive ratio = 4.52941
Tire radius = 0.298 (meter)

Acceleration force in 1st gear at max torque RPM (assuming 15% drivetrain loss) = (3.454 x 4.52941 x 155) x 85 / 100 = 6917 N

Can someone please help me to calculate the maximum slope (%) my car can climb with 6917 N force? How can I calculate rolling resistance and other negative forces?
What is the formula to calculate gradient ability?

 

[karabiner98k]

I found this picture that may be helpful:

 

[PeroK]

The simplest approach is to calculate the angle $\theta$ where $mg\sin \theta = F$, where $F = 6917N$ is the maximum drive force, $m$ is the mass of your car and $g$ is gravity ($9.8m/s^2$). I get about $36°$.

However, the other limiting factor is friction and whether you can generate that force on a sufficiently steep slope. Note that as the slope increases, so the normal force of the weight of your car on the ground reduces - it's $mg\cos \theta$. That is a factor in reducing the maximum friction you have. In any case, if the maximum friction on a slope is less than $6917N$ then that's the limiting factor.

 

[BvU]

Hi,

I'm a physicist, no specific automobile expertise, but I want to bring in some physics nevertheless:

First, the dimension of your calculated 2061 is N.m. : the 155 is N.m and the other three factors are ratios.

Then: with a wheel radius of 0.3 m, this torque would provide an accelerating force of 2060 N.m/0.3 m = 6900 N.

Such a force, if it could be fully used for acceleration would make your car accelerate with 6900 N / 1300 kg = 5.3 m/s².

Meaning you would go from 0 to 100 km/h in (100 km/h) / (3600 s/h) * (1000 m/km) / 5.32 m/s² = 5.2 seconds. (the 1300 kg is curb weight + you).

Nowadays some (rather pricey) fossil fuel cars can do this. For electric cars it's easier.

Weakest link in the reasoning: unleasing the clutch at the 4250 rpm torque maximum.
Other issue: friction has to be enough (tires must not slip).

Transfer to hill climbing capabilities:

​

F_W is the maximum acceleration force available for the wheels. It has to overcome $mg\sin\alpha$. So you would get $\sin\alpha_{\text{max}}\$= 5.3 m/s²/9.8 m/s² or $\alpha =$ 33$^\circ$.

You would go up 65 m for every 100 m driven ($\sin\alpha$). I think they call that a slope of 65 % and I wouldn't think of even trying it with my car for fear of falling over backwards

Friction required: With $F_{\text {friction, max}} = F_W = f F_N$ and $F_N = mg\cos\alpha$ you see that $f \ge \tan\alpha = 0.65$ is needed.

All in all: good question ! And fun. I hope some car buff has comments to improve the realism of these considerations

$\$

 

[PeroK]

(the 1300 kg is curb weight + you).

That's a good point: add some mass for the driver! That reduces the angle to about $33°$.

 

[BvU]

I didn't even know if curb weight includes fuel but google says it does

 

[karabiner98k]

I didn't even know if curb weight includes fuel but google says it does

Not only fuel but all the fluids of the car including radiator coolant, engine oil, power steering fluid, brake fluid, etc.

 

[PeroK]

You would go up 65 m for every 100 m driven ($\sin\alpha$). I think they call that a slope of 65 % and I wouldn't think of even trying it with my car for fear of falling over backwards

The steepest road in England is Hardknott Pass in the Lake District. It's narrow and rough as well. Never again!

https://en.wikipedia.org/wiki/Hardknott_Pass

That's 33%, or 18°.

 

[karabiner98k]

Thank you all for your responses. I also came up with 33 degrees but there are other things to consider.

As you said the main negative force here is mg* sin(θ).
I want to add some other forces to improve the precision of my calculation.
Since my car travels at only 29.5 km/h (in 1st gear @ 4250 RPM), air resistance can be neglected because the car is moving slowly.
However, I read somewhere that there is another factor called Rolling Friction.
According to the table below, we have to add 0.02 of Rolling Friction to our calculations.

I'm the driver of the car and I weigh 50 kg + 20 kg luggage at the back. So, the car weighs around 1270 kg.

Now, my question is:
How should I use that 0.02 in my calculations?
I will repeat the calculations and you can correct me if I'm wrong.

mg* sin(θ) + (mg* sin(θ) )*0.02 = ?
1270*9.81*sin(33) = 6785
6785*0.02 = 135
6785 + 135 = 6920 N

So, this is the negative force my car should overcome in order to climb a 33 degrees slope and since it has 6917 N of accelerating force, it can climb a little less than 33 degrees.
Am I right?

The steepest road in England is Hardknott Pass in the Lake District. It's narrow and rough as well. Never again!

Baldwin street in New Zealand holds the record for the steepest road in the world with a slope of 34.8% (19.2 degrees).

 

[PeroK]

These calculations are not precise enough for rolling resistance at 2% to be a factor. The margin of error is significantly more than that. I would expect air resistance, even at low speeds, to be at least as significant as rolling resistance.

The other point to note is that the drive force vs angle is probably not the critical equation.

 

[karabiner98k]

So, how can we add to the precision?

I have more information about my car if it helps:
Drag coefficient = 0.3 cd
Frontal area = 1.99 square meters

 

[PeroK]

So, how can we add to the precision?

You can't really. To go beyond the basics you need more data. How much steeper than 20 degrees could your car go? That's specialist analysis. The theoretical maximum is about 33 degrees, but where in that range you'd hit the practical maximum is anyone's guess without doing some real testing.

 

[karabiner98k]

I think these calculations are not far from truth. I tested them against official data published by well-known car manufacturers and I almost ended up with the same result!

This is an example:
Volkswagen has claimed that VW Beetle with 1600 cc engine can climb a 48% slope in 1st gear (with 2 people onboard).

Engine torque = 106 nm @ 2800 RPM
1st gear ratio = 3.80
Final Drive ratio = 4.125
Wheel radius = 0.3145 (meters)
Curb weight = 870 kg

Now, I use my own calculations to see how close I can get to the official 48% slope.
(25.64 degrees)

Drive force = 3.80*4.125*106 = 1661.55 / 0.3145 = 5283* 85% (15% drivetrain loss) = 4490 N
Car weight = 870 + 160 (2 passengers) = 1030 kg

mg* sin(25.64) + (mg* sin(25.64) )*0.02 = 4459 N

4459 N is pretty close to 4490 N!

 

[PeroK]

That's very well done! I suspect VW have done what you did and calculated the theoretical maximum gradient in each gear.

 

[jack action]

Friction required: With $F_{\text {friction, max}} = F_W = f F_N$ and $F_N = mg\cos\alpha$ you see that $f \ge \tan\alpha = 0.65$ is needed.

That is true for an AWD. It is less for a RWD or a FWD. (details)

 

[BvU]

That is true for an AWD. It is less for a RWD or a FWD. (details)

It's all worked out in the link I gave. I especially liked the last sentence

the experimentally much easier problem of determination of the angle of the inclined plane at which the drive axle slips or the car flips over.

Didn't want to complicate the thread too much. But @karabiner98k might want to use it to get a better estimate ...

 

[karabiner98k]

This is what a 60% slope looks like:

But in practice, it is not easy to climb such a steep road because even if you have the power, the weight of the car will shift to the rear axle and front axle will get lighter. The result is lower traction of front wheels and wheelspin (FWD). However, this condition may benefit RWD cars because the weight transfer increases traction at the back.

If the problem of traction (friction) can be solved, some extraordinary results can happen like this Audi which is climbing a 85% slope on a snowy surface!

 

[PeroK]

There are some steep descents as well. On a bicycle, though:

 

[anorlunda]

And then we have those who do it in competition. The car in that picture is a Subaru Forester.

 

[karabiner98k]

There was a small mistake in my calculations. I can correct it now to increase the accuracy one step further!
I said the tire radius of my car = 0.298 (meter). This is true but the real rolling radius is in fact a little smaller than that because the weight of the car compresses the tires a bit and when I pushed the car and made some measurements on the ground, one full turn of the tire was 1.815 meters (this is rolling circumference). I divided this number by 3.141 and divided the result by 2 to calculate the real rolling radius of my tires.
The real rolling radius of my tires = 0.288498 (meter)

If we repeat the calculations with the new radius, the maximum slope my car can climb would be around 34 degrees (1 degree more than before).
This shows that even a slight change in tire size can affect hill climbing ability of the car!

 

[DaveC426913]

The steepest road in England is Hardknott Pass in the Lake District. It's narrow and rough as well. Never again!

https://en.wikipedia.org/wiki/Hardknott_Pass

That's 33%, or 18°.

I don't know what the grade was but I once went up a road so steep I had to rappel back down in my van.
It was a gravel road with soft shoulders, crossing from one highway over a ridge to the next adjacent highway.

I took a run at it in my camper van, and got about halfway up before just spinning gravel. When I stopped, the van started creeping backwards down the gravel like a slow avalanche. I waited until it came to a slow halt, then eased off the brake (which I was standing on with both feet). The van started to inch backwards again, so I leaned back on the brakes, while it avalanched a few dozen feet to a stop again. Did this multiple times until I'd finally reached flat ground again.

My wife has since instigated a navigation "veto" rule.

 

[karabiner98k]

Can someone here suggest a formula for calculating air resistance force so that I can calculate slope climbing ability of my car at higher speeds?
I found a few formulas but I'm not sure which one is more accurate than others.

 

[anorlunda]

Can someone here suggest a formula for calculating air resistance force so that I can calculate slope climbing ability of my car at higher speeds?
I found a few formulas but I'm not sure which one is more accurate than others.

That's pretty difficult to calculate for a non-trivial shape. It would be far easier to measure it.

A simple way to measure is to drive on a level surface at an initial speed such as 29.5 km/h, then lift your foot off the gas and measure how quickly the car slows down. Of course that measurement lumps rolling resistance, engine/transmisison resistance, and all other kinds of friction together with air resistance, but the combined result is the meaningful one you want.But I also thought that you already concluded that it's negligible.

Since my car travels at only 29.5 km/h (in 1st gear @ 4250 RPM), air resistance can be neglected because the car is moving slowly.

 

[karabiner98k]

But I also thought that you already concluded that it's negligible.

I said it is negligible only at very slow speeds but not so at highers speeds such as 100 km/h or more.

I found this formula:

My car's frontal area = 1.99 square meters
Drag coefficient = 0.31 cd