- #1
PhizKid
- 477
- 1
I've read all sorts of descriptions in textbooks and online, but I don't get the purpose of reference frames. Why can't you just put everything on the same set of coordinate planes? I don't see what difference it makes. There was an example with a car traveling alongside another car, and that to each other, their velocities are 0. I don't get why this is because in reality they are just both traveling at the same speed. Is frame of reference just what something appears to an observer? When we solve physics problems, aren't we just observing as an omnipresent observer so that we see everything all at once?
Here is a sample question:
Car A is traveling towards the origin 800m away of an xy-plane on the positive x-axis at 80km/hr. Car B is traveling towards the origin 600m away on the same coordinate plane, but on the positive y-axis at 60km/hr.
a) Velocity of B with respect to A
b) Angle between this velocity and the line of sight between the two cars
c) If both cars maintain their velocities, do the solutions to parts a) and b) change as they move towards the origin?
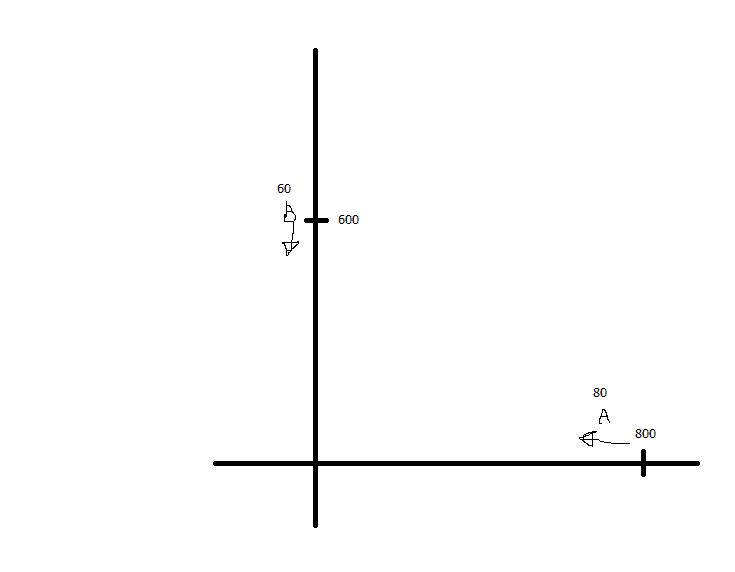
For part a), I would naturally say 60 km/hr, but it says with respect to A. So that does mean, if I am inside car A, what velocity does it look like B is traveling at to me? I know there is some equation to solve this (something like V_pA = V_pB + V_BA), but I don't understand why the equation is true or how it works. We need two frames of reference and a moving particle, but I don't know what those are in this case. Since I am the observer inside car A, I would say the p is car B, but I don't know what the reference frames B and A are. I know one reference frames is probably myself inside the car I am in? I'm not sure.
Part b) I would say 90 degrees because the vehicles are perpendicular, but I'm not sure what angle car B would look like it's at to me if I was inside car A. I guess it would look a little to my right as I'm turning my head slightly right to see the car traveling closer to me.
Part c) I guess it would change because as car B nears me, it becomes closer to my front instead of on my right side and eventually when we both reach the origin, car B will be directly in front of me or something.
Here is a sample question:
Car A is traveling towards the origin 800m away of an xy-plane on the positive x-axis at 80km/hr. Car B is traveling towards the origin 600m away on the same coordinate plane, but on the positive y-axis at 60km/hr.
a) Velocity of B with respect to A
b) Angle between this velocity and the line of sight between the two cars
c) If both cars maintain their velocities, do the solutions to parts a) and b) change as they move towards the origin?
For part a), I would naturally say 60 km/hr, but it says with respect to A. So that does mean, if I am inside car A, what velocity does it look like B is traveling at to me? I know there is some equation to solve this (something like V_pA = V_pB + V_BA), but I don't understand why the equation is true or how it works. We need two frames of reference and a moving particle, but I don't know what those are in this case. Since I am the observer inside car A, I would say the p is car B, but I don't know what the reference frames B and A are. I know one reference frames is probably myself inside the car I am in? I'm not sure.
Part b) I would say 90 degrees because the vehicles are perpendicular, but I'm not sure what angle car B would look like it's at to me if I was inside car A. I guess it would look a little to my right as I'm turning my head slightly right to see the car traveling closer to me.
Part c) I guess it would change because as car B nears me, it becomes closer to my front instead of on my right side and eventually when we both reach the origin, car B will be directly in front of me or something.