- #1
samy4408
- 62
- 9
- Homework Statement
- ...
- Relevant Equations
- ...
Sorry i don't understand English very well , if someone want to explain to me this problem?
I don't understand this problem -- Surface area of a section of a solid sphere
- Thread starter samy4408
- Start date
In summary, the problem is asking for the area of the partial sphere surface, plus the three other sides.
- #2
DaveC426913
Gold Member
- 23,070
- 6,747
What part is giving you difficulty?
Try your best to explain what you think it's asking for. We'll see of we can set you straight.
Try your best to explain what you think it's asking for. We'll see of we can set you straight.
- #3
Mark44
Mentor
- 37,796
- 10,188
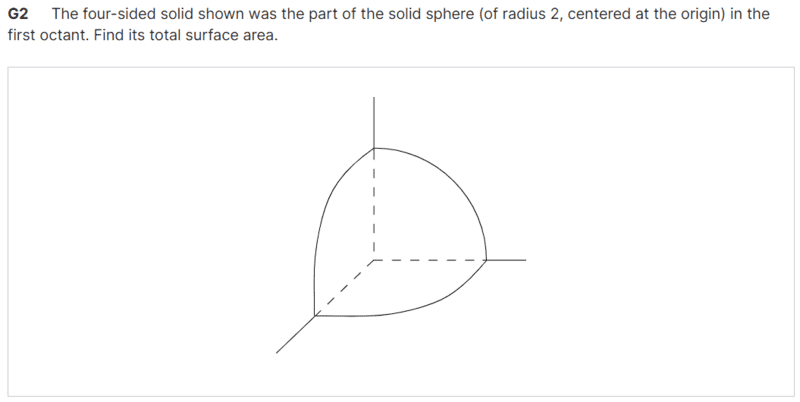
Ordinarily I would delete a post like this, as there is no work shown, but today is your lucky day.samy4408 said:
Do you know a formula for the surface area of a sphere whose radius is given?
Can you determine what fraction of a sphere is shown in the picture?
- #4
Lnewqban
Homework Helper
Gold Member
- 3,840
- 2,168
The problem is asking you to calculate the surface of a sphere that has been cut as shown.
Can you see it tridimensional in your head?
Can you see it tridimensional in your head?
- #5
samy4408
- 62
- 9
I do know the formula for the surface area of a sphere , the problem is what they are asking for ,Mark44 said:
is it the surface of the sphere that is shown ? is it 1/8 of the total surface of the sphere ?
- #6
- 19,071
- 14,729
yessamy4408 said:
- #7
Frabjous
Gold Member
- 1,845
- 2,276
No. You also have to add on the new faces from the cut.phinds said:
- #8
samy4408
- 62
- 9
So it is 2*piphinds said:
- #9
- 19,071
- 14,729
Ah. You are right of course. I missed that they want ALL of the surface area. Still a trivial problem.caz said:
- #10
Mark44
Mentor
- 37,796
- 10,188
That's just the surface area of the part of the sphere. The problem is asking for the area of the partial sphere surface, plus the three other sides.samy4408 said:
- #11
- 27,983
- 19,483
It says a "solid sphere", so this is correct, IMO. If it was just a spherical surface that was cut, it would be different.caz said:
- #12
DaveC426913
Gold Member
- 23,070
- 6,747
Well boo. You guys moved on while I was busy rendering a visual aid.
FAQ: I don't understand this problem -- Surface area of a section of a solid sphere
How do I calculate the surface area of a section of a solid sphere?
The surface area of a section of a solid sphere can be calculated by first finding the area of the full sphere using the formula A = 4πr², where r is the radius of the sphere. Then, multiply this value by the fraction of the sphere that is represented by the section. For example, if the section is a semicircle, the fraction would be 1/2.
What is the difference between surface area and volume?
Surface area refers to the total area of all the faces or surfaces of a 3-dimensional object. Volume, on the other hand, refers to the amount of space that an object occupies. In the case of a solid sphere, surface area would refer to the total area of the curved surface, while volume would refer to the amount of space inside the sphere.
Can the surface area of a section of a solid sphere be greater than the surface area of the full sphere?
No, the surface area of a section of a solid sphere will always be less than or equal to the surface area of the full sphere. This is because the section is always a fraction of the full sphere, and the surface area of a sphere increases as the radius increases.
How does the size of the section affect the surface area of a solid sphere?
The size of the section directly affects the surface area of the solid sphere. The larger the section, the greater the surface area will be. This is because a larger section represents a larger fraction of the full sphere, resulting in a larger surface area calculation.
Are there any real-world applications of calculating the surface area of a section of a solid sphere?
Yes, there are many real-world applications of calculating the surface area of a section of a solid sphere. For example, this calculation is used in engineering and construction to determine the amount of material needed to create curved structures, such as domes or arches. It is also used in physics and astronomy to calculate the surface area of planets and other celestial bodies.