EddyBenzen122
- 11
- 2
- Homework Statement
- None.
- Relevant Equations
- None.
I need help finding the resultant with vectors: 37.5N[NE] and 45N[21° S of E]
I just don't know a way to find the angles within this triangle to help me get the resultant, so can anybody help me out?
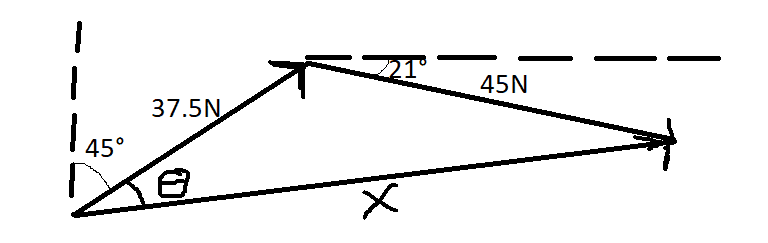
I just don't know a way to find the angles within this triangle to help me get the resultant, so can anybody help me out?