I have a question about the air volume

[Hauzen]

Hello
I need your help studying hydrodynamics.
I have a question about the volume of air.

Assuming incompressibility, non-viscosity, there is a coefficient of tube friction, and it moves in laminar flow...
The Oulet stage Fan is installed, so air moves from top to bottom. The cross-sectional area is A.
At this time, is inlet V1 and Oulet V2 the same or different?
If it's different, can it be expressed in a formula?

 

[erobz]

If the flow is non viscous, friction with pipe wall is zero. I don’t believe you can have “laminar flow” without viscosity. The shear stress at the wall is what forces the velocity gradient. Basically, One can’t keep their cake and eat it too.

But in general for “incompressible flow” and no reservoir for mass to accumulate what goes in must come out.

Hence: $$Q=A_iV_i = A_oV_o$$

However, gases like “air” are compressible and viscous, and can only be modeled as “incompressible, non-viscous” under certain conditions ( within some boundaries ).

 

[Baluncore]

If the flow is non viscous, friction with pipe wall is zero.

There is no drag, but also, there is no lift without viscosity, so the fan will not work.

 

[Lnewqban]

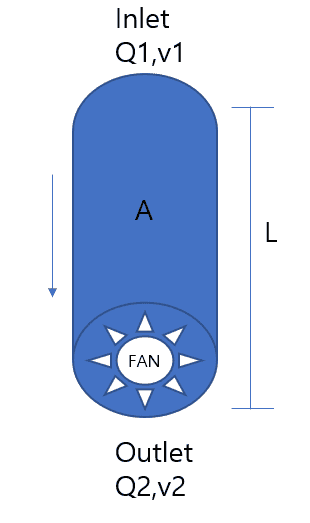
I need your help studying hydrodynamics.
I have a question about the volume of air.

Perhaps you meant fluid dynamics, which is a subdiscipline of fluid mechanics.

Hydrodynamics is the study of liquids in motion.
Aerodynamics is the study of air and other gases in motion.

Fluid mass in = Fluid mass out
Volume is a matter of density and flow distribution at each small cross-area of a cross-section.
Axial fans can make a mess of cross-sectional velocity profiles.

If the In-volume is compressed or expanded within the duct or tube, Out-volume is different to the former; but still mass in=mass out.

 

[Hauzen]

Perhaps you meant fluid dynamics, which is a subdiscipline of

Hydrodynamics is the study of liquids in motion.
Aerodynamics is the study of air and other gases in motion.

Fluid mass in = Fluid mass out
Volume is a matter of density and flow distribution at each small cross-area of a cross-section.
Axial fans can make a mess of cross-sectional velocity profiles.

If the In-volume is compressed or expanded within the duct or tube, Out-volume is different to the former; but still mass in=mass out.

View attachment 341569
View attachment 341570

Thank you so much for the CFD interpretation
I understood that very well.
I'm sorry, but let me ask you one more question.
I understand m1=m2, but is it a part that can be proved by the Q1>Q2 hydrodynamic formula?

 

[Lnewqban]

...
I understand m1=m2, but is it a part that can be proved by the Q1>Q2 hydrodynamic formula?

You are welcome.
What Q1 and Q2 stand for?
Is it simply velocity times cross-sectional area, as shown in post #2 above?

 

[Ron_H]

There is no drag, but also, there is no lift without viscosity, so the fan will not work.

So can you rotate the fan? If so: What happens when you rotate the fan? Does it require torque to rotate the fan? What does this fluid do when you rotate the fan?

 

[Baluncore]

Birds and insects cannot fly without fluid viscosity. The fan has airfoil shaped blades, so air cannot be moved unless the air has viscosity.
https://en.wikipedia.org/wiki/D'Alembert's_paradox

Liu, T. Evolutionary understanding of airfoil lift. Adv. Aerodyn. 3, 37 (2021).
https://aia.springeropen.com/counter/pdf/10.1186/s42774-021-00089-4.pdf
Conclusions; Lift is generated only in a viscous flow, which naturally coexists with the viscous drag. Without the fluid viscosity, both lift and drag are zero (D′Alembert’s paradox).

 

[Ron_H]

So can you rotate the fan? If so: What happens when you rotate the fan? Does it require torque to rotate the fan? What does this fluid do when you rotate the fan?

Birds and insects cannot fly without fluid viscosity. The fan has airfoil shaped blades, so air cannot be moved unless the air has viscosity.
https://en.wikipedia.org/wiki/D'Alembert's_paradox

Liu, T. Evolutionary understanding of airfoil lift. Adv. Aerodyn. 3, 37 (2021).
https://aia.springeropen.com/counter/pdf/10.1186/s42774-021-00089-4.pdf
Conclusions; Lift is generated only in a viscous flow, which naturally coexists with the viscous drag. Without the fluid viscosity, both lift and drag are zero (D′Alembert’s paradox).

Birds and insects cannot fly without fluid viscosity. The fan has airfoil shaped blades, so air cannot be moved unless the air has viscosity.
https://en.wikipedia.org/wiki/D'Alembert's_paradox

Liu, T. Evolutionary understanding of airfoil lift. Adv. Aerodyn. 3, 37 (2021).
https://aia.springeropen.com/counter/pdf/10.1186/s42774-021-00089-4.pdf
Conclusions; Lift is generated only in a viscous flow, which naturally coexists with the viscous drag. Without the fluid viscosity, both lift and drag are zero (D′Alembert’s paradox).

So let’s say that there is no lift without viscosity. Does that imply no fan can move the fluid? Think about the questions I asked before.

 

[Baluncore]

So let’s say that there is no lift without viscosity. Does that imply no fan can move the fluid?

This is the paradox of an inviscid fluid. It takes no effort to turn the fan. The fluid simply flows around the fan blades as they pass through the air. But this contradicts the changes in kinetic energy as the mass of air moves around the blade, and dynamic air pressure is still a real thing.

Accept that real air has viscosity, and the problem is gone.

 

[Ron_H]

I'm assuming you are correct. But I can't track with you. Here's where I am: The blades have an angle of attack. So there seems to be no way to rotate the fan without accelerating the fluid. That tells me it takes torque to turn the fan. Where did I go wrong?

 

[Baluncore]

Where did I go wrong?

You have assumed air is inviscid, but you know it has viscosity.
Read the wiki article on D'Alembert's paradox.
https://en.wikipedia.org/wiki/D'Alembert's_paradox

 

[Hauzen]

You are welcome.
What Q1 and Q2 stand for?
Is it simply velocity times cross-sectional area, as shown in post #2 above?

I'm sorry for the late response because it's Korean time.
Yes, that’s right.
Assuming that it is a pipe that descends vertically, and that the lower fan rotates to draw air from top to bottom (at low speed, close to incompressibility), I would like to prove how the inlet airflow Q1 and the outlet airflow Q2 differ.
In fact, I would like to prove that the air volume (Q1) of Inlet and the air volume (Q2) of Outlet are different in the duct designed as shown above.
Is it a part that can be logically proved by Bernoulli's formula or other theory?
I'd like to prove it with a formula.

 

[Ron_H]

You have assumed air is inviscid, but you know it has viscosity.
Read the wiki article on D'Alembert's paradox.
https://en.wikipedia.org/wiki/D'Alembert's_paradox

Thanks for the link. I didn’t know about the paradox. I think it was a given (not my assumption) that this fluid is inviscid.

So the article says that there is no *drag* in our problem.

But it does not say that there is no lift.

Picturing a ceiling fan with non-zero pitch, I still see fluid being accelerated axially. And I still don’t see fluid accelerating without work.

Where’s my mistake?

 

[erobz]

Assuming that it is a pipe that descends vertically, and that the lower fan rotates to draw air from top to bottom (at low speed, close to incompressibility), I would like to prove how the inlet airflow Q1 and the outlet airflow Q2 differ.

"close to incompressibility" implies $Q_1$ and $Q_2$ do not differ in any substantial way. It seems like an inconsistent question is being asked.

 

[Baluncore]

Assuming incompressibility, non-viscosity, there is a coefficient of tube friction, and it moves in laminar flow...

The OP wrongly assumed that there was no viscosity. That contradicted the OP assumption of there being "tube friction".

So the article says that there is no *drag* in our problem.

Which "article"?
What is "our problem"?

Picturing a ceiling fan with non-zero pitch, I still see fluid being accelerated axially. And I still don’t see fluid accelerating without work.

An inviscid fluid will be pushed out of the way by the fan blade, the fluid will then flow back in behind the blade, without loss of energy to heat or turbulence.
Acceleration is balanced by deceleration. There is a net-zero energy balance.

The paper I linked in post #8, discusses the dependence of lift on viscosity, in section 6.

 

[Ron_H]

The OP wrongly assumed that there was no viscosity. That contradicted the OP assumption of there being "tube friction".


Which "article"?
What is "our problem"?


An inviscid fluid will be pushed out of the way by the fan blade, the fluid will then flow back in behind the blade, without loss of energy to heat or turbulence.
Acceleration is balanced by deceleration. There is a net-zero energy balance.

The paper I linked in post #8, discusses the dependence of lift on viscosity, in section 6.

“The paper I linked in post #8, discusses the dependence of lift on viscosity, in section 6.“

Got it! Wonderful! Thanks very much for your patience.

 

[Hauzen]

"close to incompressibility" implies $Q_1$ and $Q_2$ do not differ in any substantial way. It seems like an inconsistent question is being asked.

There's something that's hard for me to understand.
Assuming an incompressible fluid is flowing, friction would reduce the static pressure. Is there a moment when the length of the pipe is infinite and the static pressure becomes zero? I wonder if the dynamic pressure would decrease at that time.

 

[erobz]

There's something that's hard for me to understand.
Assuming an incompressible fluid is flowing, friction would reduce the static pressure. Is there a moment when the length of the pipe is infinite and the static pressure becomes zero? I wonder if the dynamic pressure would decrease at that time.

The dynamic pressure is the equal at both ends of the pipe.

 

[erobz]

Imagine you have a horizontal pipe of length $x$. Applying the "Energy Equation" ( a formulation of the First Law of Thermodynamics under certain simplifying assumptions )

$$ \frac{P_1}{\rho g } + z_1 + \frac{V_1^2}{2g} = \frac{P_x}{\rho g } + z_x + \frac{V_x^2}{2g} + \sum_{1 \to x } h_{loss} $$

Simplify. No change in elevation inlet to outlet $z_1 = z_x$, hence:

$$ \frac{P_1}{\rho g } + \cancel{z_1} + \frac{V_1^2}{2g} = \frac{P_x}{\rho g } + \cancel{z_x} + \frac{V_x^2}{2g} + \sum_{1 \to x } h_{loss} $$

$$ \frac{P_1}{\rho g } + \frac{V_1^2}{2g} = \frac{P_x}{\rho g } + \frac{V_x^2}{2g} + \sum_{1 \to x } h_{loss} $$

Next assumption: Incompressible flow ( uniformly distributed velocity across inlet/outlet for simplicity ):

$$\dot m_1 = \dot m_2$$

$$ \cancel{\rho} A_1 V_1 =\cancel{\rho} A_x V_x $$

With $A_1 = A_x$, $V_1 = V_x$, hence:

$$ \frac{P_1}{\rho g } + \cancel{\frac{V_1^2}{2g}} = \frac{P_x}{\rho g } + \cancel{\frac{V_x^2}{2g}} + \sum_{1 \to x } h_{loss} $$

i.e. Dynamic pressure at 1 is equal to dynamic pressure at $x$.

Caneling terms, we are left with(re-arranging):

$$ \frac{P_1- P_x}{\rho g } = \overbrace{\sum_{1 \to x } h_{loss}}^{\text{Heat}>0} $$

So if $P_x$ is 0 gage (atmosphere), we simply have that at the end of the pipe ( position $x$) all the static pressure at $P_1$ is converted to heat.

 

[Hauzen]

Imagine you have a horizontal pipe of length $x$. Applying the "Energy Equation" ( a formulation of the First Law of Thermodynamics under certain simplifying assumptions )

$$ \frac{P_1}{\rho g } + z_1 + \frac{V_1^2}{2g} = \frac{P_x}{\rho g } + z_x + \frac{V_x^2}{2g} + \sum_{1 \to x } h_{loss} $$

Simplify. No change in elevation inlet to outlet $z_1 = z_x$, hence:

$$ \frac{P_1}{\rho g } + \cancel{z_1} + \frac{V_1^2}{2g} = \frac{P_x}{\rho g } + \cancel{z_x} + \frac{V_x^2}{2g} + \sum_{1 \to x } h_{loss} $$

$$ \frac{P_1}{\rho g } + \frac{V_1^2}{2g} = \frac{P_x}{\rho g } + \frac{V_x^2}{2g} + \sum_{1 \to x } h_{loss} $$

Next assumption: Incompressible flow ( uniformly distributed velocity across inlet/outlet for simplicity ):

$$\dot m_1 = \dot m_2$$

$$ \cancel{\rho} A_1 V_1 =\cancel{\rho} A_x V_x $$

With $A_1 = A_x$, $V_1 = V_x$, hence:

$$ \frac{P_1}{\rho g } + \cancel{\frac{V_1^2}{2g}} = \frac{P_x}{\rho g } + \cancel{\frac{V_x^2}{2g}} + \sum_{1 \to x } h_{loss} $$

i.e. Dynamic pressure at 1 is equal to dynamic pressure at $x$.

Caneling terms, we are left with(re-arranging):

$$ \frac{P_1- P_x}{\rho g } = \overbrace{\sum_{1 \to x } h_{loss}}^{\text{Heat}>0} $$

So if $P_x$ is 0 gage (atmosphere), we simply have that at the end of the pipe ( position $x$) all the static pressure at $P_1$ is converted to heat.

Wow! thank very much!!!
Thank you for your detailed explanation.
I understood it perfectly when I expressed it in a formula like this.

 

[erobz]

Wow! thank very much!!!
Thank you for your detailed explanation.
I understood it perfectly when I expressed it in a formula like this.

Just know that if you are doing any specific problem, the set of assumptions that lead the "Energy Equation" may not be valid. I leave it up to you to research and find out what is ok for what in a specific application.

 

[Lnewqban]

... I would like to prove how the inlet airflow Q1 and the outlet airflow Q2 differ.
In fact, I would like to prove that the air volume (Q1) of Inlet and the air volume (Q2) of Outlet are different in the duct designed as shown above.

That will be very difficult to prove, because Q1 and Q2 are equal.

Please, see:
https://en.wikipedia.org/wiki/Continuity_equation#Fluid_dynamics