- #1
SPiZ
- 2
- 0
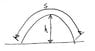
How do I find out what angle to fire a projectile so that the height it attains is equiv to the length of its arc? Whats a general formula? Assume the projectile is "fired" from ground level. Say, from a pea shooter or a sling shot.