I need a Straight Compact Linear data model

[1plus1is10]

Does anyone know a model to identify Straight Compact Linear data?

I've been toying with Pearson Correlation Coefficient and am very disappointed.
https://en.wikipedia.org/wiki/Pearson_correlation_coefficient
I originally thought that this would be exactly what I needed, but...
After some Googling, I soon discovered Anscombe's quartet.
https://en.wikipedia.org/wiki/Anscombe's_quartet

Frank Anscombe basically said "look at your data". Duh.

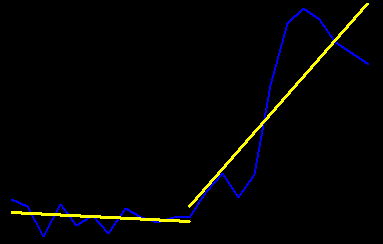
Per online calculator: https://www.socscistatistics.com/tests/pearson/Default2.aspx
The first line's PCC is: -0.2679=bad. The X values are 1-12 and the Y values are:
53
46
19
48
29
38
22
44
36
32
36
36

The second line's PCC is: 0.8358=good. The Y values are:
36
60
76
54
75
156
212
226
216
195
185
175

I need a model where the first line is good and the second is bad.
Any ideas?

 

[1plus1is10]

PS... Straight can be up or down also, not just flat. As long as it is compact and straight.

 

[1plus1is10]

After toying with this some more and also stopping to ask, "what do I actually see", I think I now understand the problem:
= It's all relative (it's all about scale).

Basically, if I look at each side of my graph independently, then the PCC results make much more sense.
More specifically, the top and bottom of the graph for the first line's data changes and the data no longer looks compact.
This is due to scale - it's no longer relative to the second line's data.

So, having realized the problem, I thought some more and stared at it some more, and I think I have a solution (for me anyway).
My solution actually has 2 parts:
1) Iterate through the entire data with a fixed/desired sample size to get an average Standard Deviation. Then use it as a comparison.
2) Do a Quadratic Regression of the desired data to calculate it's Latus Rectum and divide it by the sample size. The bigger the percent, the straighter the data.

If anyone can think of a better hammer, I'd still like to hear from you.
(my eyes see that there has to be something regarding crossovers, but I got nothing yet)
Thanks