I with matlab designing a steady state feedback H2 control system

[Nahahahah]

Hi everyone.
I'm designing a steady state feedback H2 control system.
Actually, my major is tribology and I have no experience in designing control system.
So it is really big problem for me.
Anyway, this is my simple model of tribometer which applies normal load on the surface.

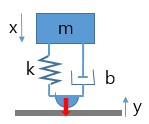
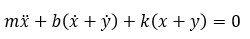(is it right??)
My purpose is control the x (position of m) during the test (change in y) to apply constant normal load (k(x+y) ??) on the surface.
When I start the test, the normal force will be kx, but during the test the movement of substrate(y) occurs and I want to control the position of x to maintain constant normal load on the substrate.
And I should design state feedback controller with H2 norm minimized via LMI optimization.

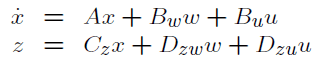with

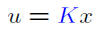
First, I thought disturbance (w) is y and output z will be k(x+y)... but I failed.
I really need some help to design the state feedback controller.
Thanks!

 

[scottdave]

It's been awhile for me, but here goes. Let's start with (Net Force) = mass * acceleration, which in your case acceleration is x double dot. So should your first equation equal zero? If you set it equal to the driving force (the force you are applying to keep it at desired position) then that seems what you need to solve. Is gravity acting downward on the mass? If so then you should have that in there as a downward external force on the mass.