Ideal Gas Behavior: Choose the Right Diagram

[b_andries]

Hi guys,

Can someone explain me please how to find the following question?
Which diagram represents the behavior of an ideal gas the most?

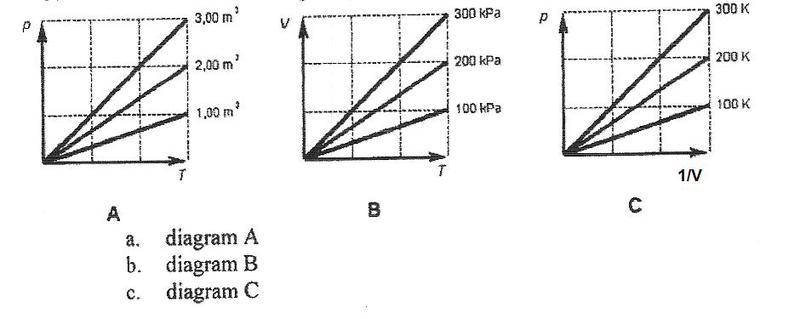
I know it's C but I don't know why. They all seem to represent the behavior of a ideal gas.
But why C mor than the others?

Thanks

 

[Andrew Mason]

What is the equation that relates P, V and T for an ideal gas?

What is the relationship between P and T if V is constant (first graph)?

What is the relationship between V and T if P is constant (second graph)?

What is the relationship between P and 1/V if T is constant (third graph)?

AM

 

[b_andries]

What is the equation that relates P, V and T for an ideal gas?

P.V = n.R.T

What is the relationship between P and T if V is constant (first graph)?
==>T instead of V is constant here no(same values on x-axis)?

P.V = n.R. = constant so this should be wrong because there is a slope

What is the relationship between V and T if P is constant (second graph)?
isn't here also T constant instead of P?

V = n.R /P
So if V rises than P has to decline
This graph would not be possible because T is constant and P and V both rise.What is the relationship between P and 1/V if T is constant (third graph)?

Volume here is constant(same values on x-axis)
P= n.R.T (So if P rises T has to Rise too)
In this case they both rise so it would also be possible

 

[Andrew Mason]

What is the equation that relates P, V and T for an ideal gas?

P.V = n.R.T

You don't need the .'s. Just: PV = nRT

What is the relationship between P and T if V is constant (first graph)?
==>T instead of V is constant here no(same values on x-axis)?

No. P is on the y-axis and T is on the x axis. Each line represents the points (P,T) for which V has the same value (that value is stated at the end of the line).

What is the relationship between V and T if P is constant (second graph)?
isn't here also T constant instead of P?

No. V is on the y-axis and T is on the x axis. Each line represents the points (V,T) for which P has the same value (that value is stated at the end of the line).

What is the relationship between P and 1/V if T is constant (third graph)?

Volume here is constant(same values on x-axis)

No. P is on the y-axis and 1/V is on the x axis. Each line represents the points (P,1/V) for which T has the same value (that value is stated at the end of the line).

AM

 

[b_andries]

Ok thanks,

Now i know what I've done wrong

 

[Andrew Mason]

Ok thanks,

Now i know what I've done wrong

Can you explain why c) is the correct answer (and why a) and b) do not fit: PV=nRT?)

AM

 

[b_andries]

P(1/V)= nRT 1/V (function P with respect to 1/V)
So here nRT represents the slope of the graph
A larger Temperature gives a larger slope, which is what diagram C shows
So diagram C is correct.


P(T) = nR/V T(function P with respect to T)
So nR/V represents the slope of the graph
A Larger volume should give smaller slope, but in diagram A, larger V gives larger slope.
So diagram A is wrong.


V(T) = nR/P T(function V with respect to T)
So nR/P represents the slope of the graph
A Larger Pressure should give a smaller slope, but in diagram B, larger Pressure gives a larger slope.
Thus diagram B is wrong.

Am I correct?

 

[Andrew Mason]

P(1/V)= nRT 1/V (function P with respect to 1/V)
So here nRT represents the slope of the graph
A larger Temperature gives a larger slope, which is what diagram C shows
So diagram C is correct.


P(T) = nR/V T(function P with respect to T)
So nR/V represents the slope of the graph
A Larger volume should give smaller slope, but in diagram A, larger V gives larger slope.
So diagram A is wrong.


V(T) = nR/P T(function V with respect to T)
So nR/P represents the slope of the graph
A Larger Pressure should give a smaller slope, but in diagram B, larger Pressure gives a larger slope.
Thus diagram B is wrong.

Am I correct?

Yes. Very well explained.

AM