vcsharp2003
- 913
- 179
- Homework Statement
- How does a real mass pulley system differ from an ideal mass pulley system when applying Newton's Second of Law of motion?
- Relevant Equations
- F = ma and Torque = r X F
Below is an ideal mass pulley system that we encounter in many problems under Newton's Second Law of Motion questions.
Its supposed to be massless and frictionless i.e. string slips over the pulley and pulley does not rotate.
I think bullet#3 is the correct explanation because tension does not act on the pulley but on the string. We are looking at the pulley only as the system and therefore, we are interested in forces acting on the pulley and not on the string.
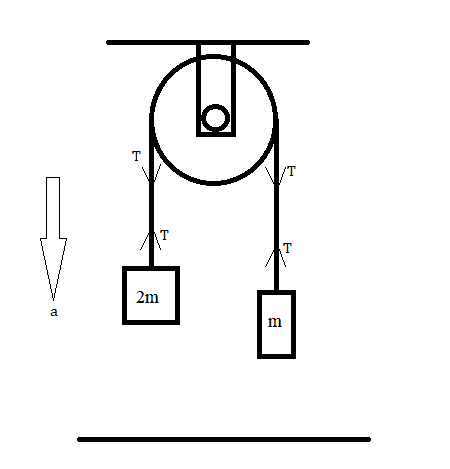
Its supposed to be massless and frictionless i.e. string slips over the pulley and pulley does not rotate.
- In a real system, the pulley is assumed to be massless, whereas in reality it does have some mass and therefore some moment of inertia.
- In a real system, the pulley string contact surface would not be frictionless, so the string will not slip over the pulley causing the pulley to rotate. Perhaps, the string could also slip in some cases where coefficient of static friction is very low between string and pulley?
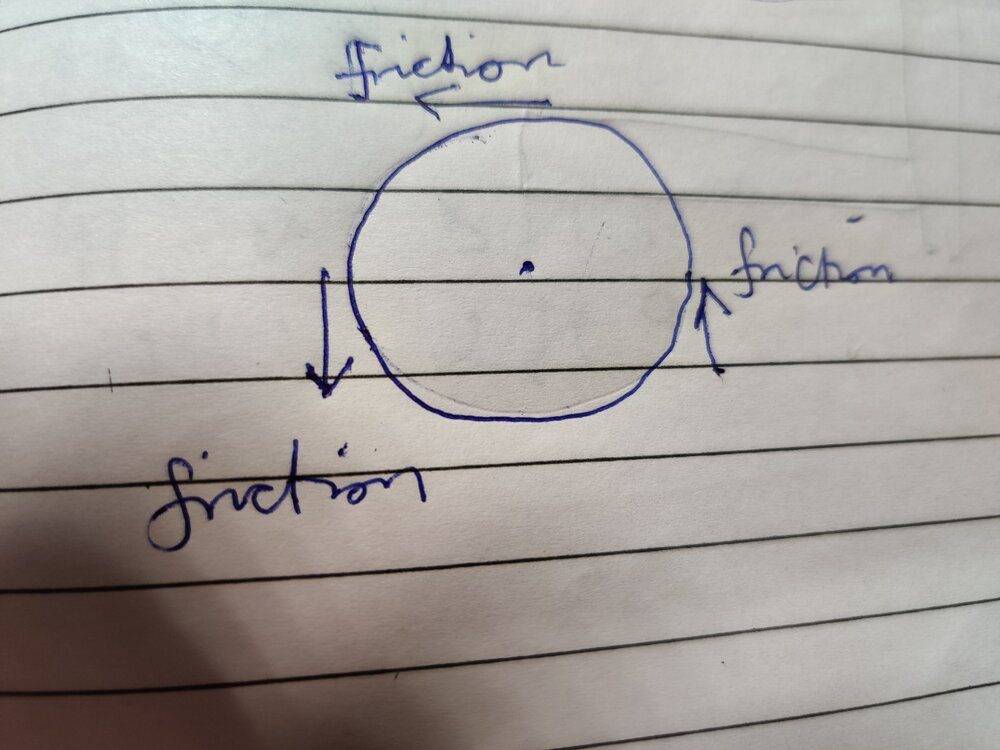
- In a real system, the friction force on the pulley ( not on the string) would be acting downwards on left side of the pulley and upwards on the right side of the pulley. On the top part of the pulley this friction force would act in leftwards direction. It is this friction force that would cause the pulley to rotate counter clockwise.
- In a real system, the reason why pulley would rotate is because the tensions are unequal on left side and right sides of the string over the pulley. The left side tension would be greater than the right side tensions resulting in a net counter clockwise torque that would cause the pulley to rotate counter clockwise.
I think bullet#3 is the correct explanation because tension does not act on the pulley but on the string. We are looking at the pulley only as the system and therefore, we are interested in forces acting on the pulley and not on the string.
Last edited: