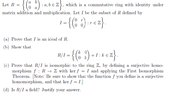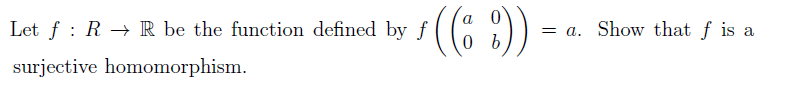Ideals and Ker(f) Solution for (a), (b), and (c)

[Joe20]

I have attached my solution for part (a), (b) and (c). I am not sure if part (a), (b) are correct. However for part (c), the question did not define the output of the function so I am not sure if I can do it as such as I do not know how to continue. Therefore need verification on all the 3 parts. Thanks!

 

[Euge]

Your proofs for parts (a) and (b) look good. Your solution to (c), however, does not make sense. To prove (c), define an explicit map $f : R \to \Bbb Z$, and show that it’s a surjective ring homomorphism with kernel $I$. The result then follows from the first isomorphism theorem for rings.

Consider $f : R\to \Bbb Z$ given by $f(A) = A_{12}$, where $A_{12}$ is the $(1,2)$-entry of $A$. Show that $f$ has the desired properties.

 

[Joe20]

Your proofs for parts (a) and (b) look good. Your solution to (c), however, does not make sense. To prove (c), define an explicit map $f : R \to \Bbb Z$, and show that it’s a surjective ring homomorphism with kernel $I$. The result then follows from the first isomorphism theorem for rings.

Consider $f : R\to \Bbb Z$ given by $f(A) = A_{12}$, where $A_{12}$ is the $(1,2)$-entry of $A$. Show that $f$ has the desired properties.

Hi, what does the 1,2 entry means? Am I right to say it is incorrect to prove surjective and homomophism from what I have thus far?

 

[Euge]

Hi, what does the 1,2 entry means? Am I right to say it is incorrect to prove surjective and homomophism from what I have thus far?

The $(1,2)$-entry of $A$ means the entry in the first row and second column of $A$.

 

[Joe20]

Hi, I have included an e.g. of showing of f:R -> R (real no) being defined by the function to be a. In my question above, it was not being defined. So am I going to define it myself? How am I going to define it in order to prove for surjective homorphism? [it stated as f: R -> Z (integer)]

 

[Euge]

No, you want $f: R \to \Bbb Z$ given by $f\left[\begin{pmatrix}a&b\\0&a\end{pmatrix}\right] = a$. That's what I meant earlier, but had a typo (it was supposed to read $f(A) = A_{11}$, not $f(A) = A_{12}$).

 

[Joe20]

No, you want $f: R \to \Bbb Z$ given by $f\left[\begin{pmatrix}a&b\\0&a\end{pmatrix}\right] = a$. That's what I meant earlier, but had a typo (it was supposed to read $f(A) = A_{11}$, not $f(A) = A_{12}$).

I have revised it to as attached. Is it correct now? [Note: I only show the proof till surjective homomorphism, I shall continue once this is correct].

I am still somehow confused with f:R→Z given by f((a b)¦(0 a ))=a.(why can't it be f((a b)¦(0 a ))=b)?

 

[Euge]

You have proven correctly that $f$ is a ring homomorphism, but you have not proved correctly that $f$ is surjective. Elements of $R$ are matrices of the form $\begin{pmatrix}a&b\\0&a\end{pmatrix}$, so matrices like $\begin{pmatrix}a&0\\0&0\end{pmatrix}$ where $a\neq 0$ do not belong to $R$.

The reason you can't make $f : R\to \Bbb Z$ be $f\left[\begin{pmatrix}a&0\\0&a\end{pmatrix}\right] = a$ is because not all elements of $R$ are of the form $\begin{pmatrix}a&0\\0&a\end{pmatrix}$. The matrix $\begin{pmatrix}1&1\\0&1\end{pmatrix}$, for example, belongs to $R$. Look back at the definition of $R$.

 

[Joe20]

You have proven correctly that $f$ is a ring homomorphism, but you have not proved correctly that $f$ is surjective. Elements of $R$ are matrices of the form $\begin{pmatrix}a&b\\0&a\end{pmatrix}$, so matrices like $\begin{pmatrix}a&0\\0&0\end{pmatrix}$ where $a\neq 0$ do not belong to $R$.

The reason you can't make $f : R\to \Bbb Z$ be $f\left[\begin{pmatrix}a&0\\0&a\end{pmatrix}\right] = a$ is because not all elements of $R$ are of the form $\begin{pmatrix}a&0\\0&a\end{pmatrix}$. The matrix $\begin{pmatrix}1&1\\0&1\end{pmatrix}$, for example, belongs to $R$. Look back at the definition of $R$.

Thanks. Btw, I am not sure how to see if R/I is a field or not. May need help.

 

[Euge]

Since $R/I$ is ring isomorphic to $\Bbb Z$, one can just say that since $\Bbb Z$ is not a field, $R/I$ is not a field. Of course, proving part (d) does not require use of the isomorphism. It is enough to show that the coset $\begin{pmatrix}2&0\\0&2\end{pmatrix} + I$ has no inverse.

 

[Joe20]

Since $R/I$ is ring isomorphic to $\Bbb Z$, one can just say that since $\Bbb Z$ is not a field, $R/I$ is not a field. Of course, proving part (d) does not require use of the isomorphism. It is enough to show that the coset $\begin{pmatrix}2&0\\0&2\end{pmatrix} + I$ has no inverse.

May I ask how do we know that the coset has no inverse?

 

[Euge]

It follows from the fact that there is no integer solution to the equation $2a = 1$. By the way, just to be clear, by “inverse” I meant multiplicative inverse, not additive inverse.

 

[Joe20]

It follows from the fact that there is no integer solution to the equation $2a = 1$. By the way, just to be clear, by “inverse” I meant multiplicative inverse, not additive inverse.

Thank you so much! I got it now.