Identifying Vertical Asymptotes: A Non-Factoring Method

[Teh]

View attachment 6087
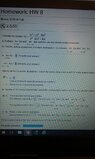
im stuck on identifying vertical asymptotes because of this nasty denominator. My professor telling me to factor it out but, is there different way to solve for the vertical asymptotes.

 

[topsquark]

im stuck on identifying vertical asymptotes because of this nasty denominator. My professor telling me to factor it out but, is there different way to solve for the vertical asymptotes.

Other than graphing, not that I know of.

You need to factor [math]x^4 - 61x^2 + 900[/math]. If you set [math]y = x^2[/math] then you have to factor [math]y^2 - 61y + 900[/math]. Are you able to do that?

-Dan

 

[Teh]

i did! for the denominator it is (x+5) (x+6) (x-5) (x-6) for the top i am not sure

 

[Prove It]

i did! for the denominator it is (x+5) (x+6) (x-5) (x-6) for the top i am not sure

Surely you can at least see some common factors...

 

[Teh]

yes also did tried it this is what i got 2x^2 (x^2 + x - 30) is equal to 2x^2 (x-6) (x+5)... then cancel it out with (x-6) (x+5)

 

[MarkFL]

Your factorization of the numerator is close, but not quite correct...check your signs. :D

 

[Teh]

ahhh okay (x+6) and (x-5) canceling with (x+6) (x-5) leaving 2x^2 / (x-6) (x+5)