Hill
- 735
- 575
Consider this proof:
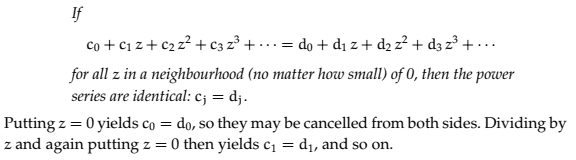
Is it a valid proof?
When we divide by ##z##, we assume that ##z \neq 0##. So, we cannot put ##z=0## on the next step. IOW, after dividing by ##z## we only know that $$c_1+c_2z+c_3z^2+...=d_1+d_2z+d_3z^2+...$$ in a neighborhood of ##0## excluding ##0##.
Is it a valid proof?
When we divide by ##z##, we assume that ##z \neq 0##. So, we cannot put ##z=0## on the next step. IOW, after dividing by ##z## we only know that $$c_1+c_2z+c_3z^2+...=d_1+d_2z+d_3z^2+...$$ in a neighborhood of ##0## excluding ##0##.
Last edited: