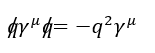Identity with Gamma matrices and four-vector contractions

[Francisco Alegria]

TL;DR Summary

I want to determine a specific identity involving gamma matrix and four vectors

Is the fowwowin identity correct for a generic four-vector"q"? What is the proof? Thank you.

 

[vanhees71]

That's "Diracology". You need the defining property of the $\gamma$ matrices,
$$\{\gamma^{\mu},\gamma^{\nu} \}=2 \eta^{\mu \nu}.$$
Your expression can be written as (with the Einstein summation convention in action)
$$\begin{split}
q_{\alpha} q_{\beta} \gamma^{\alpha} \gamma^{\mu} \gamma^{\beta}&=q_{\alpha} q^{\beta} \left (\gamma^{\alpha} \{\gamma^{\mu},\gamma^{\beta} \} - \gamma^{\alpha} \gamma^{\beta} \gamma^{\mu} \right) \\ &= q_{\alpha} q_{\beta} \left (2\gamma^{\alpha} \eta^{\mu \beta} - \frac{1}{2} \{\gamma^{\alpha} ,\gamma^{\beta} \} \gamma^{\mu} \right)\\
&=2q_{\alpha} \gamma^{\alpha} q^{\mu} - q^2 \gamma^{\mu}.
\end{split}$$
[Note: Is there some equivalent of "slashed" from the LaTeX package slashed.sty to type "Feynman slashes"?]

 

[Demystifier]

[Note: Is there some equivalent of "slashed" from the LaTeX package slashed.sty to type "Feynman slashes"?]

$\not{\!p}$ is produced by typing "\not{\!p}".