lorenz0
- 151
- 28
- Homework Statement
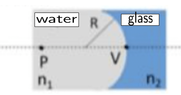
- A spherical glass lens of radius ##R=20cm## with refraction index ##n_2=1.5## is placed underwater. Find the position of the image placed at ##p=50cm## from the vertex ##V## and the magnification of the image.
- Relevant Equations
- ##\frac{n_1}{p}+\frac{n_2}{1}=\frac{n_2-n_1}{R}##, ##M=\frac{n_1 q}{n_2 p}##
Using the data given and recalling that in this configuration ##R<0## I get: ##\frac{1.33}{0.5}+\frac{1.5}{q}=\frac{1.5-1.33}{-0.2}\Rightarrow q\approx -0.427 m=-42.7 cm## so the image is virtual and is ##42.7\ cm## to the left of vertex ##V##. The magnification is ##M=\frac{n_1 q}{n_2 p}=\frac{1.33\cdot (-0.427)}{1.5\cdot 0.5}\approx -0.757## so the image is shorter (##\approx 75.7\%##) than the original and is upside down.
Is this correct? Thanks.
Is this correct? Thanks.