- #1
Master1022
- 611
- 117
- Homework Statement
- What is the correct form of the Laplacian filter in image processing?
- Relevant Equations
- Laplacian
Hi,
I just have a quick question regarding image processing. What is the correct form of the Laplacian for image processing?
I have seen different versions online and don't understand which one is meant to be the conventional one. I know that:
[tex] \nabla^2 f(x, y) = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} [/tex]
Type 1:
[tex] \begin{pmatrix} 2 & -1 & 2 \\ -1 & -4 & -1 \\ 2 & -1 & 2 \\ \end{pmatrix} [/tex]
I believe this is derived by forming matrices for the second derivative in the x and y-directions separately and then combining those matrices. This one does that across all the 3 rows/columns.
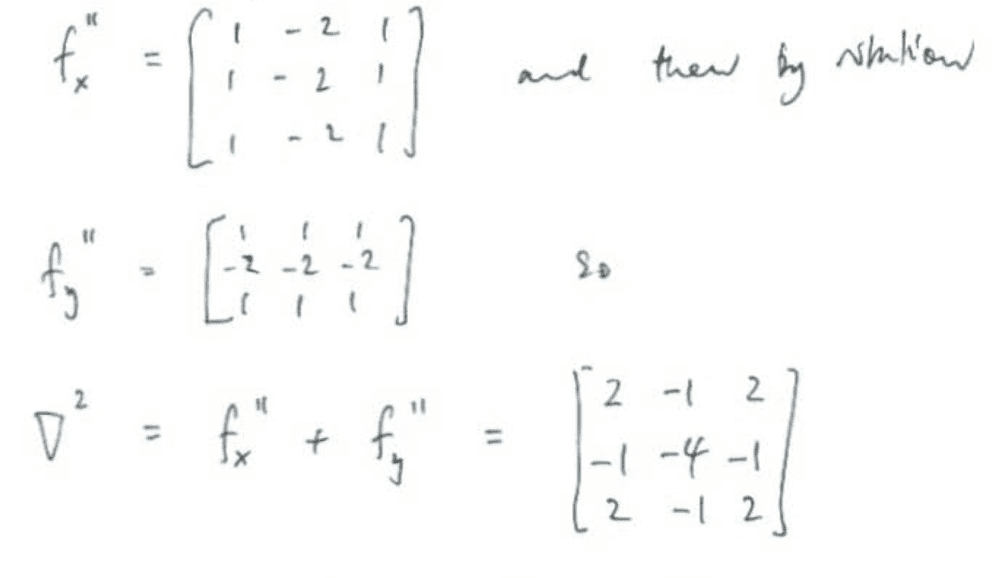
Type 2:
[tex] \begin{pmatrix} 0 & -1 & 0 \\ -1 & -4 & -1 \\ 0 & -1 & 0 \\ \end{pmatrix} [/tex]
This one is derived by doing the same as above, but only populating the central row/column.
Any help would be greatly appreciated.
I just have a quick question regarding image processing. What is the correct form of the Laplacian for image processing?
I have seen different versions online and don't understand which one is meant to be the conventional one. I know that:
[tex] \nabla^2 f(x, y) = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} [/tex]
Type 1:
[tex] \begin{pmatrix} 2 & -1 & 2 \\ -1 & -4 & -1 \\ 2 & -1 & 2 \\ \end{pmatrix} [/tex]
I believe this is derived by forming matrices for the second derivative in the x and y-directions separately and then combining those matrices. This one does that across all the 3 rows/columns.
Type 2:
[tex] \begin{pmatrix} 0 & -1 & 0 \\ -1 & -4 & -1 \\ 0 & -1 & 0 \\ \end{pmatrix} [/tex]
This one is derived by doing the same as above, but only populating the central row/column.
Any help would be greatly appreciated.