- #1
John Greger
- 34
- 1
Hi everyone,
I was thinking about the complex part of the dielectric function. To my understanding there's good physical explanation of it. is a superimposed description of dispersion phenomena occurring at multiple frequencies.
Say I only have the real part such as the one below, and would like to get (approximately) the imaginary part. How could I obtain a plot of it, by just looking at the below figure? As using the Kramers-Kronig relation is rather tedious if you only want to get a sense of the behaviour.
I found the following statement: " the imaginary part leads to absorption loss if it is positive (in the above sign convention) and gain if it is negative." But I'm not sure how this would translate into a plot of the real part below?
Thanks in advance.
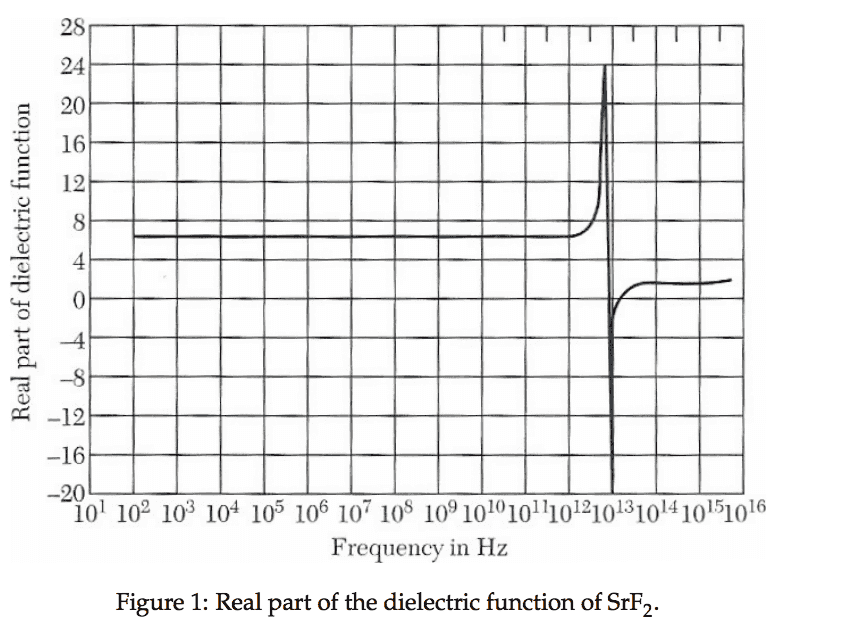
I was thinking about the complex part of the dielectric function. To my understanding there's good physical explanation of it. is a superimposed description of dispersion phenomena occurring at multiple frequencies.
Say I only have the real part such as the one below, and would like to get (approximately) the imaginary part. How could I obtain a plot of it, by just looking at the below figure? As using the Kramers-Kronig relation is rather tedious if you only want to get a sense of the behaviour.
I found the following statement: " the imaginary part leads to absorption loss if it is positive (in the above sign convention) and gain if it is negative." But I'm not sure how this would translate into a plot of the real part below?
Thanks in advance.