IMC-Based PID Controller Design for Second Order Process - Homework Solution

[gfd43tg]

Homework Statement

Homework Equations

The Attempt at a Solution

Hello,
I know for a second order process, the tuning parameters are given as $k_{c} = \frac {\tau_{1}+\tau_{2}}{k_{p} \lambda}$, $\tau_{I} = \tau_{1} + \tau_{2}$, and $\tau_{D} = \frac {\tau_{1}+\tau_{2}}{\tau_{1} \tau_{2}}$

syms s
lambda = 1;
kp = -0.2735;
gp = kp/(s^2+6.035*s+4.146);
[num,den] = numden(gp);
factors = eval(solve(den,s));
tau1 = factors(1); tau2 = factors(2);
kc = (tau1+tau2)/(kp*lambda)
tauI = tau1+tau2
tauD = (tau1+tau2)/(tau1*tau2)

These are my process time constants

tau1 =

  -0.7906

tau2 =

  -5.2444

This gives my controller parameters

kc =

  22.0658tauI =

  -6.0350tauD =

  -1.4556

I go into simulink, and here is my model

And here are my PID controller inputs

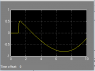
But I haven't figured out why my controller is not working, here is the output

 

[gfd43tg]

I realized that $\tau_{D} = \frac {\tau_{1} \tau_{2}}{\tau_{1} + \tau_{2}}$, but still my output is not correct even after changing my $\tau_{D}$ term

 

[gfd43tg]

I figured it out. My time constants were not correct or in the right form