- #1
dsdsuster
- 30
- 0
Hi,
The book I'm reading references the fact that the impedance seen by the inverting input of an inverting amplifier is just the two feed back resistors, R1 and R2 in parallel.
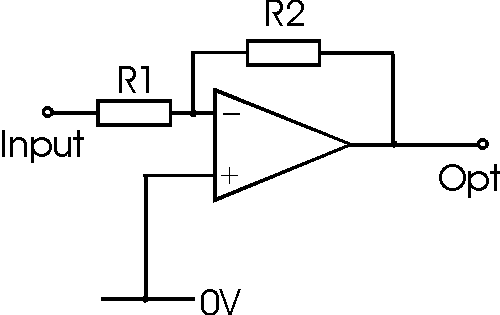
I'm having trouble seeing this. I understand how the basic voltage divider with one end at Vin and the other at ground can be replaced by its Thevenin equivalent but in this case it seems like the tail of R2 is connected just to some arbitrary output terminal. In fact ground is actually connected to the non-inverting input and it seems to me there's no easy way to create a Thevenin equivalent of the driving source without examining the opamp's innards.
The book goes as far as to redraw the inverting amplifier with the Input voltage in series with (R1,R2 parallel) connected to the inverting terminal with nothing connected to the opamp output so we are essentially have open loop gain. Surely this cannot be equivalent? To give some context, we are looking at the effects of input biasing currents so the Input voltage is grounded. I apologize if this last paragraph is confusing since I can't supply a picture.
My main question is just in what sense is it true that the impedance seen by the inverting input of an inverting amplifier is just the two feed back resistors, R1 and R2 in parallel? I'm struggling to reconcile this with my understanding of the more traditional voltage divider.
Thank you
The book I'm reading references the fact that the impedance seen by the inverting input of an inverting amplifier is just the two feed back resistors, R1 and R2 in parallel.
I'm having trouble seeing this. I understand how the basic voltage divider with one end at Vin and the other at ground can be replaced by its Thevenin equivalent but in this case it seems like the tail of R2 is connected just to some arbitrary output terminal. In fact ground is actually connected to the non-inverting input and it seems to me there's no easy way to create a Thevenin equivalent of the driving source without examining the opamp's innards.
The book goes as far as to redraw the inverting amplifier with the Input voltage in series with (R1,R2 parallel) connected to the inverting terminal with nothing connected to the opamp output so we are essentially have open loop gain. Surely this cannot be equivalent? To give some context, we are looking at the effects of input biasing currents so the Input voltage is grounded. I apologize if this last paragraph is confusing since I can't supply a picture.
My main question is just in what sense is it true that the impedance seen by the inverting input of an inverting amplifier is just the two feed back resistors, R1 and R2 in parallel? I'm struggling to reconcile this with my understanding of the more traditional voltage divider.
Thank you
