- #1
Calcifur
- 24
- 2
Hi all,
I have a question which I think should be a simple solve for most people but I cannot seem to get my head around it.
It is a common case in geophysical surveying that a magnetic field vertical gradiometer might be used.
This instrument uses two magnetometers separated by a known distance (along the vertical axis) and calculates the magnetic field gradient by subtracting the magnetic total field measured at one from the other (unit: ΔTeslas) then dividing by their separation distance (unit: metres or feet) (i.e. ΔB/Δx).
Gradiometers are often used in geophysics for detecting ferrous anomalies below the Earth's surface by measuring the anomaly's effect on the local magnetic field without the need to filter out smaller scale diurnal, or geological variations. It has its uses for buried object detection and rare mineral exploration etc.
To clarify once more, a local magnetic field gradient is calculated by the following formula:
B1= The magnetic field reading for the first (i.e. Top) magnetometer (in nT).
B2= The magnetic field reading for the second (i.e. Bottom) magnetometer (in nT).
z= The vertical separation.
Currently, I am employed on a survey using a vertical gradiometer that outputs only the final vertical gradient value (Grad) and not the original measurements i.e. B1 and B2 (Hard to believe, I know! ).
).
The vertical separation between magnetometers is exactly 1ft), i.e. Grad =(B1-B2)/1ft meaning it's output units are in ΔnT/Δft. The problem is I need the value in ΔnT/Δm.
... I thought that this would be an easy fix: 1m= 3.28084ft meaning ΔnT/Δm = (ΔnT/Δft)*3.28084.
However, I suspect this isn't correct due to the fact that I know the magnetic field fall off rate is not a linear relationship.
The magnetic field measured by a magnetometer for an anomaly degrades with sensor to anomaly distance by an inverse cube relationship, thereby meaning if the centre position of the gradiometer was constant but the separation was increased, Magnetometer B1 would be increased in height, and B2 would decrease. B1's field readings would decay at a rate of B1^-3 with distance as the sensor moves away from the object, B2 would increase at a rate of B2^3.
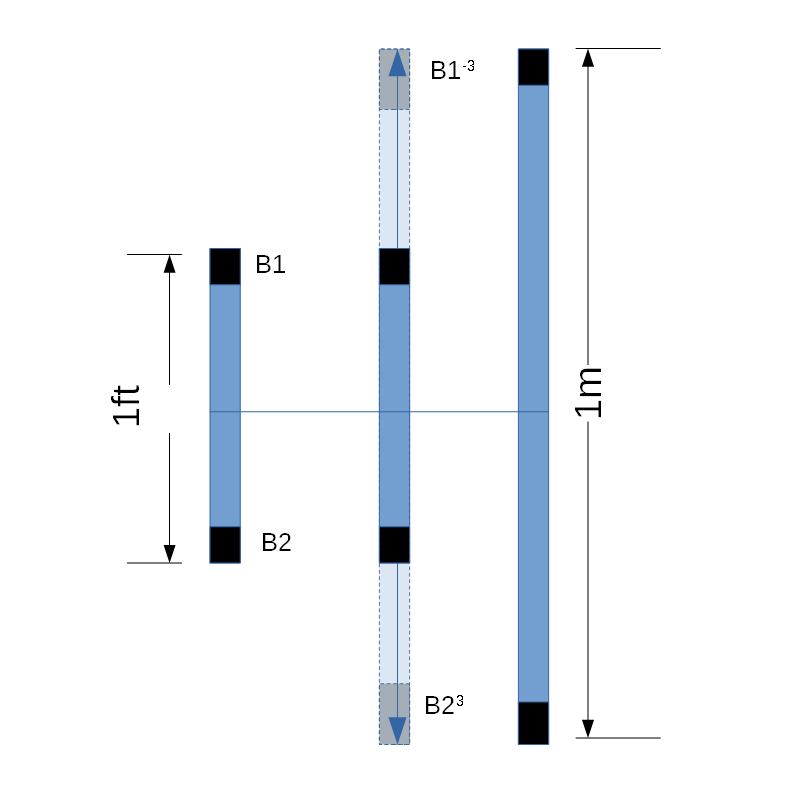
My question is this: Do I need to factor the above relationship into my conversion from ΔnT/Δft to ΔnT/Δm ? If so, how do I do this?
Many thanks in anticipation guys, you always help me out in a jam!
Calcifur
I have a question which I think should be a simple solve for most people but I cannot seem to get my head around it.
It is a common case in geophysical surveying that a magnetic field vertical gradiometer might be used.
This instrument uses two magnetometers separated by a known distance (along the vertical axis) and calculates the magnetic field gradient by subtracting the magnetic total field measured at one from the other (unit: ΔTeslas) then dividing by their separation distance (unit: metres or feet) (i.e. ΔB/Δx).
Gradiometers are often used in geophysics for detecting ferrous anomalies below the Earth's surface by measuring the anomaly's effect on the local magnetic field without the need to filter out smaller scale diurnal, or geological variations. It has its uses for buried object detection and rare mineral exploration etc.
To clarify once more, a local magnetic field gradient is calculated by the following formula:
Grad =(B1-B2)/z
Where:B1= The magnetic field reading for the first (i.e. Top) magnetometer (in nT).
B2= The magnetic field reading for the second (i.e. Bottom) magnetometer (in nT).
z= The vertical separation.
Currently, I am employed on a survey using a vertical gradiometer that outputs only the final vertical gradient value (Grad) and not the original measurements i.e. B1 and B2 (Hard to believe, I know!
The vertical separation between magnetometers is exactly 1ft), i.e. Grad =(B1-B2)/1ft meaning it's output units are in ΔnT/Δft. The problem is I need the value in ΔnT/Δm.
... I thought that this would be an easy fix: 1m= 3.28084ft meaning ΔnT/Δm = (ΔnT/Δft)*3.28084.
However, I suspect this isn't correct due to the fact that I know the magnetic field fall off rate is not a linear relationship.
The magnetic field measured by a magnetometer for an anomaly degrades with sensor to anomaly distance by an inverse cube relationship, thereby meaning if the centre position of the gradiometer was constant but the separation was increased, Magnetometer B1 would be increased in height, and B2 would decrease. B1's field readings would decay at a rate of B1^-3 with distance as the sensor moves away from the object, B2 would increase at a rate of B2^3.
My question is this: Do I need to factor the above relationship into my conversion from ΔnT/Δft to ΔnT/Δm ? If so, how do I do this?
Many thanks in anticipation guys, you always help me out in a jam!
Calcifur