Implementing FDM Boundary Conditions at a Red Point

[Hosein Javanmardi]

TL;DR Summary

confused about the boundary equation in the form of FDM at a node located right at the interface of three areas with different permeabilities.

in Finite Difference Method (FDM), the boundary conditions can be implemented by applying the continuity of parallel component of magnetic field intensity. when it comes to the interface of two areas, it is done at ease, but consider this case at the red point:

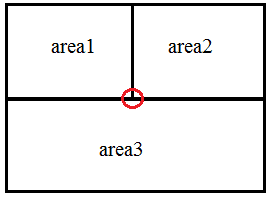
in FDM we exactly require on equation for each node. however in this case, both $H_x$ and $H_y$ components must be continous. although I am confused about the equation at this node, I cannot find one equation to satisfy all conditions at this point.
any suggestions? thanks.

 

[Paul Colby]

One of the things I've done in the past is use interpolation to express the field at a point midway between the intersection point and the closest sample point along the boundary. The boundary condition is then applied to this interpolated point which by its definition resides between just two regions.

 

[Hosein Javanmardi]

thank you Mr Colby for sharing knowledge. it seems genius to use interpolation, I don't know how to formulate. but thus far I have written this equation based on Ampere's circuit law around the singular node:
$$-2hH_x(x_b,y_b^-)+hH_y(x_b^-,y_b^+)+hH_x(x_b^-,y_b^+)+hH_x(x_b^+,y_b^+)-hH_y(x_b^+,y_b^+)=0$$
where $H_x$ and $H_y$ denote the x and y component of magnetic field intensity and $x_b^-$and $x_b^+$ and $y_b^-$ and $y_b^+$ are the x and y coordinates of the singular node. the superscript (+) and (-) means for left and right derivatives when writing $H$ in terms of $A_z$ derivatives. and $h$ is the mesh size.
do you think it is correct? if not please tell me about the interpolation equation at this node.

 

[Paul Colby]

Two questions. What boundary conditions are you applying on the outer boundary? Away from all boundaries what are your equations exactly?

 

[Hosein Javanmardi]

Hello again. the actual problem is more complicated. in order to realize a more realistic one, I will add a fourth area above (1) and (2).

in this example the equations are as following:
in area (1) and (3) and (4):
$$\nabla^2A_z=0$$
in area (2):
$$\nabla^2A_z=f$$
where $f$ is a given nonhomogeneous function due to permanent magnet.
materials in each area:
(1)=soft magnetic($\mu_{r1}=2000$),
(2)=permanent magnet magnetized in x direction($\mu_{r2}=1.05$),
(3) and (4)= non magnetic material($\mu_{r3}=mu_{r4}=1.00$)
the boundary conditions on the left, above and bottom outer edges is dirichlet:
$$A_z=0$$
on the right outer edge it is symmetry condition:
$$A_z(x-h,y)=A_z(x+h,y)$$

 

[Paul Colby]

This is very close to the 2D problem I did so many years ago ($A_z=E_z$ and $f=0$). My suggestion is to select your grid so the interior boundaries are centered half way in between grid points[1]. Use interpolation between regions of continuous quantities to determine them on the boundary. As I recall there were points at which I used extrapolation to fill in points where interpolation wasn't an option (points at which $E_z = 0$ for example). Another difference I used square grid but allowed boundaries to be general lines.

[1] the reason to do this is so the center of every computational molecule is an interior point. For example if a point x is near a boundary at which $E_z=0$ then an extrapolation through x to a point on the boundary must yield 0. Adjust $E_z$ at x accordingly.

 

[Hosein Javanmardi]

thank you again Mr. Colby. to use linear interpolation, is it enough to say:
$$4A_z(x_b,y_b)=A_z(x_b-h,y_b)+A_z(x_b+h,y_b)+A_z(x_b,y_b-h)+A_z(x_b,y_b+h)$$
although I was wondering that this interpolation plot would lead to the same laplace equation. and it is in contrast with the magnetostatic boundary condition.
the half way mesh sizing technique is also interesting. but I am intentionally placing nodes on the interfaces to achieve the most accurate left and right derivatives for the boundary condition.
I'm really interested to find the physical boundary equation. however this answer really helped. thank you again.

 

[Paul Colby]

Recall that only interior points obey the differential equation, $\nabla^2A_z = f$. If $x_b$ refers to a boundary or interface point, then I don't think your equation is what you want since it's treating the boundary as an interior point. Some of the derivatives are not continuous across the boundary. On the boundary the values are either fixed by the problem or you must express them in terms of values at points on the interior by applying the boundary condition (on tangent H for example).

As I recall I was doing a time stepping calculation, not an elliptic one like yours. There was a time step which updated values followed by a boundary condition correction step. To do this in your case requires the equations you are seeking be included in your system matrix.

In your case $H_x = \frac{\partial A_z}{\partial y}$ is continuous across a horizontal boundary but discontinuous across a vertical one. You know this discontinuity exactly from the constitutive relations. Similar situation for $H_y$.

Some depends on your solution method. Is it iterative or direct for example. If it's iterative then it might be possible to split the iteration into one that updates the interior region assuming known boundary values followed by an interpolation step to fix the boundary conditions using the interior values.

 

[Hosein Javanmardi]

Yes, I know that the laplace equation is valid only on interior nodes. all that you mentioned is completely correct. but I was just wondering how come the linear interpolation method and the discrete laplace equation on the node will result the same equation(if my interpolation was correct).
by the way how can I accept your answer? it seems physics forum is a little different than other websites like stackexchange. thanks.

 

[Paul Colby]

I was just wondering how come the linear interpolation method and the discrete laplace equation on the node will result the same equation(if my interpolation was correct).

I don't believe they will be the same. They can't be because not all second derivatives of $A_z$
exist on the boundary.

how can I accept your answer?

No worries. PF is more of a discussion than a here's your answer site. I haven't given any answers just ways I've done similar things in the past. Without working your problem completely, I don't know the answer. There is likely more than one for that matter.