Mohmmad Maaitah
- 90
- 20
- Homework Statement
- Write the two equations of equilibrium (Do not solve)
- Relevant Equations
- ((Newton's second law))
I can't find the angle between F(Big arrow in my drawing) and the y-axis!
I am terrible in geometry, what book do you suggest to me as Mechanical Engineer to get better at geometry??
This is my attempt to solution and the figure:
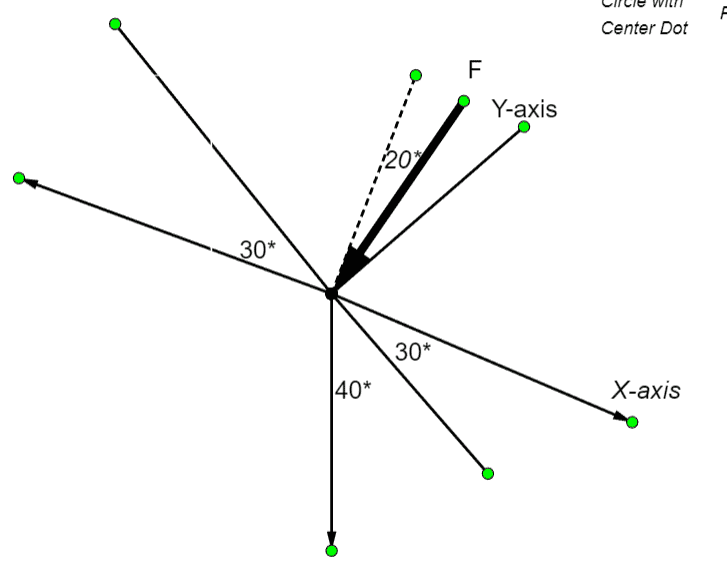
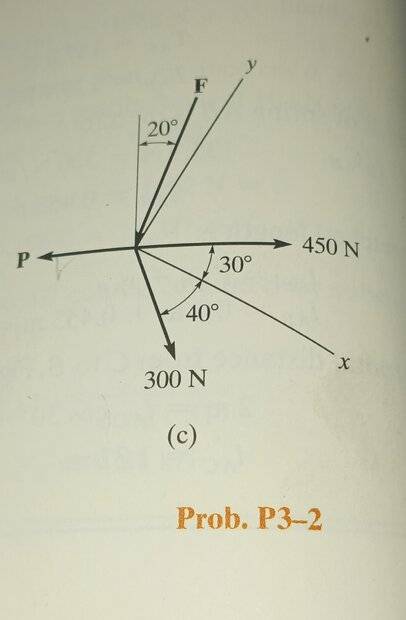
I am terrible in geometry, what book do you suggest to me as Mechanical Engineer to get better at geometry??
This is my attempt to solution and the figure: