- #1
SohailS
- 5
- 0
Hello, I am taking physics 12U through correspondence. I am having issues with this problem. I don't know why but I feel like I made a mistake in this. Can you guys check this question and verify my results.
Thanks, very much.
A baseball with a mass of 0.152 kg is moving horizontally at 32.0 m/s [E], when it is struck by a bat for 0.00200 seconds. The velocity of the ball just after the collision is 52.0 m/s [W 20° N].
Given:
Break down vectors into components
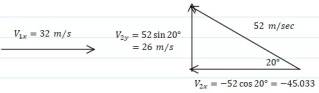
solve for components
Thanks, very much.
Homework Statement
A baseball with a mass of 0.152 kg is moving horizontally at 32.0 m/s [E], when it is struck by a bat for 0.00200 seconds. The velocity of the ball just after the collision is 52.0 m/s [W 20° N].
a) Find the impulse experienced by the ball. (6 marks)
b) Find the average net force of the ball. (2 marks)
Given:
[itex]m_{} = 0.152 kg[/itex]
[itex]v_{1} = 32.0 m/s [E][/itex]
[itex]t{} = 0.00200 s[/itex]
[itex]v_{2} = 52 m/s [W 20° N][/itex]
Homework Equations
[itex]\vec{ΔP}=\vec{F}_{NET}Δt[/itex]
[itex]F_{NET}Δt=m(v_{2}-v_{1})[/itex]
The Attempt at a Solution
a)
[itex]\vec{ΔP}=?[/itex]
[itex]F_{NET}Δt=m(v_{2}-v_{1})[/itex]
Break down vectors into components
solve for components
[itex]\vec{P}_{x}=0.152(-45.033-32)=-11.7 Ns[/itex]
[itex]\vec{P}_{y}=0.152(26-0)=39.52 Ns[/itex]
[itex]P=\sqrt{(-11.7)^{2}+(39.52)^{2}}=41.2 Ns[/itex]
[itex]θ=tan^{-1}\frac{39.52}{11.7}=73°[/itex]
[itex]∴\vec{ΔP}=41.2 Ns [W 73° N][/itex]
b)
[itex]F_{NET}Δt=41.2 Ns[/itex]
[itex]\vec{F}_{NET}=\frac{41.2}{0.002}=20,609 N [W 73° N] [/itex]