- #1
DaTario
- 1,091
- 45
- TL;DR Summary
- Is there any theoretical prediction in QM regarding the increase of coherent length through a series of stimulated emissions as it seems to happen in the linear cavity of a ruby laser setup?
Hi All,
When I teach the basic structure of a laser setup, stimulated emission appears as a fundamental phenomenon. But in no reference I found a description that could account for the increase of coherent length of the EM laser field. According to my knowledge, one photon typically doesn't have even 1% of the coherence length of a laser beam. Sometimes I wonder if in each stimulated emission, the photon released by the atom stimulated by the passing resonant photon couples with it in a way that enlarges a bit the coherent length (as in situation B of figure bellow). But the most frequently found illustration for stimulated emission is similar to figure A.
My question is:
Is there any theoretical prediction in QM that aims at providing an elementary explanation of this increase of spatial coherence? Is there any reference that deals with this subject specifically?
Best Regards,
DaTario
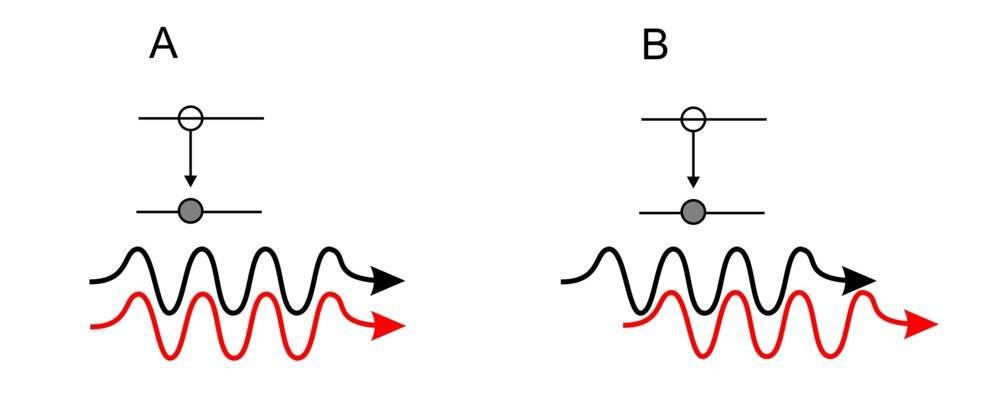
When I teach the basic structure of a laser setup, stimulated emission appears as a fundamental phenomenon. But in no reference I found a description that could account for the increase of coherent length of the EM laser field. According to my knowledge, one photon typically doesn't have even 1% of the coherence length of a laser beam. Sometimes I wonder if in each stimulated emission, the photon released by the atom stimulated by the passing resonant photon couples with it in a way that enlarges a bit the coherent length (as in situation B of figure bellow). But the most frequently found illustration for stimulated emission is similar to figure A.
My question is:
Is there any theoretical prediction in QM that aims at providing an elementary explanation of this increase of spatial coherence? Is there any reference that deals with this subject specifically?
Best Regards,
DaTario