Increase Tension in String: Rigid Rod, Weight, and Length

[karis]

Homework Statement

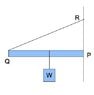
A light rigid rod PQ is hinged smoothly to the wall at one end while the other end is connected by an inextensible string to a point R directly above P. A weight W is suspended from a point on the rod. If the rod remains horizontal, which of the following change(s) would increase the tension in the string?

(1) Shifting the weight towards Q
(2) Replacing the string with a shorter one and connecting it to the mid-points of PQ and PR
(3) Replacing the string with a longer one and connecting it to a point higher than R

Homework Equations

The Attempt at a Solution

I guess the first one is correct, as the force will be greater when W is farer away from the hinged point, but i have no idea how the length of the string is related to the tension.
Is it related to the L/g ^1/2?

Please help:(
many thanks

 

[rl.bhat]

If T is the tension in the string, when the rod is horizontal, the moments on the rod due to T and W are equal and opposite.
So
(Tsinθ)*L = W*x.
T = W*x/L*sinθ . sinθ
In this expression W and L remain constant.
Your guess for the first one is correct.
sinθ = y/sqrt(L^2 + y^2). Hence
T = W*x*sqrt(L^2 + y^2)/L*y.
Now try for (2) and (3)