Induced EMF within a part of a parallel circuit?

[PhiowPhi]

A Power supply is connected to a parallel circuit with resistance R, there are three wires connected in parallel where the voltages would be the same,however, the current would be dived based on the number of wires and the resistance is the same.

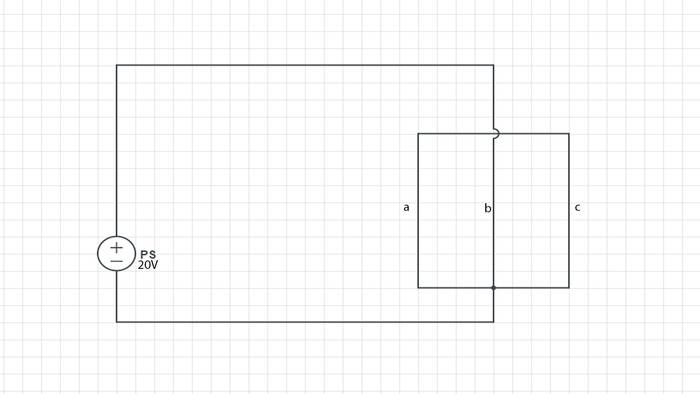
What would happen if wire (c) was placed in a changing magnetic field, and there is an induced EMF as diagram here:

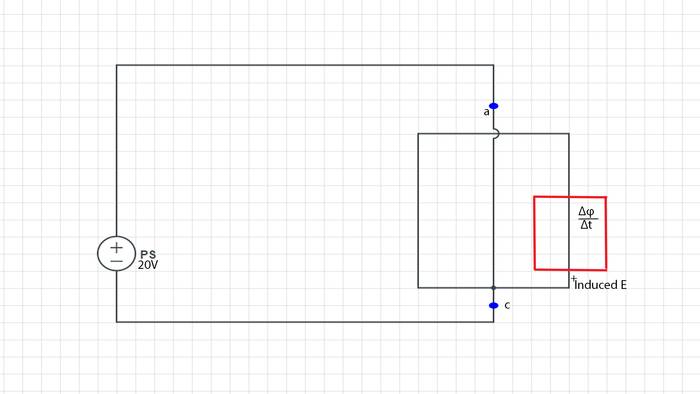
With two cases, one the polarity is opposing the power supply and and the other case is the induced EMF's polarity supporting the power supply as the diagram above.

What is the resulting voltage? If the induced EMF is opposing the power supply then the EMF would be: $V_ps - V_e$, and if the voltage is supporting the power supply(as the second diagram) the voltage is added?

I could not predict the outcome when thinking about the theory.

 

[Svein]

The way you have drawn it, there is no connection between the upper part of b and the upper part of a - c.

 

[NascentOxygen]

That "hump" in your wiring should be a connection of all 3 wires.

Perhaps it may be clearer were you to draw 3 resistors in those wires, then show the induced emf as though it is a battery added into that wire. See how that affects things.

 

[PhiowPhi]

My apology for the terrible diagrams re-adjusted them based on your comments:
Induced EMF opposing the power supply:

Induced EMF supporting the power supply:

I could not be certain of the outcome, for the first diagram where the induced-EMF is opposing the power supply I assumed that the voltage would be 15, and from the second diagram I assumed it to be 25V, however, not sure what is correct. Also, could not figure out the voltage at the blue points(a,c).

 

[Svein]

In the upper diagram, the "induced E" will almost short-circuit the power supply. The voltage between a and c will be forced to 5V.

The lower diagram isn't much better, since the PS will try to force +20V between a and c. As drawn, the "induced E" will definitely short-circuit the power supply.

 

[jim hardy]

Svein is saying "doesn't that wire going from upper right 'c' down to 6 volt source have some resistance ? "

 

[PhiowPhi]

Yes, it does.

 

[Svein]

Svein is saying "doesn't that wire going from upper right 'c' down to 6 volt source have some resistance ? "

Yes, it does.

OK. Look at the upper diagram. Let us assume a very thin wire and assign it a resistance of 0.1Ω. The current through that wire will then be (20V - 5V)/0.1Ω = 150A. Something is definitely going to break!

 

[NascentOxygen]

Don't bother posting your revised circuit. I intended for you to sketch it on paper and examine it by yourself. 3 wires, 3 resistances, with that extra battery in series with one of them. What is going to be different then?

 

[PhiowPhi]

Don't bother posting your revised circuit. I intended for you to sketch it on paper and examine it by yourself. 3 wires, 3 resistances, with that extra battery in series with one of them. What is going to be different then?

Its kind of frustrating that with all the time I've invested into understanding circuit theory I can't come up with a proper answer.

 

[jim hardy]

Looks like a good time label some currents and write Kirchoff's laws equations around the loops...

Nobody works these in their head until they've been at it for a semester or two.

 

[PhiowPhi]

Sure I'll give it a try, but isn't this a short-circuit? As Svein stated it.

 

[jim hardy]

OK. Look at the upper diagram. Let us assume a very thin wire and assign it a resistance of 0.1Ω.

looks to me like a 0.1 ohm resistor not a short circuit.

In beginner courses a short circuit is zero ohms.
When one moves on to real life "short circuit analysis", the resistance (and inductance) of the wiring comes into play.
That's why you'll never get infinite amps out of your wall socket, but you might get a thousand for a millisecond or two.

 

[PhiowPhi]

looks to me like a 0.1 ohm resistor not a short circuit.

In beginner courses a short circuit is zero ohms.
When one moves on to real life "short circuit analysis", the resistance (and inductance) of the wiring comes into play.
That's why you'll never get infinite amps out of your wall socket, but you might get a thousand for a millisecond or two.

But wouldn't the existence of the induced-EMF on wire (c), cause a short circuit? Or would it change the overall voltage... not so sure I'll play around with KVL&KCL, and will share my results and see where I'm wrong.

 

[jim hardy]

But wouldn't the existence of the induced-EMF on wire (c), cause a short circuit?

How ?

KVL and KCL will not fail you. Admittedly it's hard work when we're new to it but
what does not kill us , strengthens us.

 

[PhiowPhi]

How ?

Not sure, just a gut feeling.

what does not kill us , strengthens us.

Daily motto.

 

[PhiowPhi]

I worked on a few attempts and here is my answer: Based on the wires resistance being the same(in fact for the whole circuit), the voltages for wire a/b would be 20V and 15V for wire c due to the induced-EMF opposing the power supply, and 25V when its non-opposing.

Here is the most confusing part, the current. I think that the current would divide out based on each wire's voltage. PS is at 20V/100V = 0.2A/3 = 0.06A
However, because the last wire has lower PD it should be getting much less then that value(Not sure how to find that even with KCL and KVL). The same assumption goes when the induced-emf is non-opposing 25V would require higher current than the other wires.

 

[PhiowPhi]

Also, would the voltage still be 20V all around for both circuits. I am confused now with the induced-EMF changing the PD for the whole circuit? Or the single wire?

 

[jim hardy]

I worked on a few attempts and here is my answer: Based on the wires resistance being the same(in fact for the whole circuit), the voltages for wire a/b would be 20V and 15V for wire c due to the induced-EMF opposing the power supply, and 25V when its non-opposing.

Well, looks like you successfully applied KVL ... Hooray !

Here is the most confusing part, the current. I think that the current would divide out based on each wire's voltage. PS is at 20V/100V = 0.2A/3 = 0.06A

Say what ?

Focus on the three legs one at a time.
What is voltage across R1 ? What does Ohm's law say the current must be through R1 ?
Repeat for other two resistances.
Then sum currents by KCL.

This is how we work problems, one baby step at a time. Redraw between each step , gradually building up the number of known quantities and reducing the number of unknowns.

Everybody wants to leap straight to the answer. But it is no more possible to do that than to climb stairs one whole flight at a time.

 

[PhiowPhi]

Although you advice

Well, looks like you successfully applied KVL ... Hooray !

That's fun, but I'm missing out on something. See point c should be the voltages across the resistor + the induced emf non-opposing the circuit, or the voltages across the resistors - opposing voltage. I'm looking at point(c) as v-out

Say what ?

Ignore the confusing muble dumble!

Focus on the three legs one at a time.
What is voltage across R1 ? What does Ohm's law say the current must be through R1 ?
Repeat for other two resistances.
Then sum currents by KCL.

This is how we work problems, one baby step at a time. Redraw between each step , gradually building up the number of known quantities and reducing the number of unknowns.

Everybody wants to leap straight to the answer. But it is no more possible to do that than to climb stairs one whole flight at a time.

Golden. I'll try it out again and comeback, thank you for trying to make me learn instead of taking the answer without even understanding as to how or why things are. The same goes for @NascentOxygen

I appreciate all participation!

 

[jim hardy]

You know, i suffer terribly from "fear of failure" and "fear of frustration" . It causes me to fluster about instead of digging into problems.
That is the weak side of my nature trying to avoid the emotional pain of making a mistake. Somehow that weak side of me thinks it'll preserve my vanity to not even try.

Awareness of that flaw in my makeup keeps me on the lookout for the behavior. Symptom is I'll throw up all kinds of reasons why i cannot solve the problem confronting me.
I have this saying that i tell myself when i find myself flustering about:
"The easiest way out is straight through. "

Pride when swallowed is quite nourishing.

Success consists in large part of having a big inventory of little mistakes from which we've learned.

So, plug & chug those formulas. It is a huge mistake to not teach our "gut feel" about them.

old jim

 

[PhiowPhi]

@jim hardy Could help clarify my misconception of how this is not a short-circuit?
If you look at my last diagrams, point (c) would be the voltage from the power supply across all the resistor and the induced voltage( when non-opposing) and should be remaining voltage across the resistors - the induced voltage(when opposing), why wouldn't a short circuit be a possibility here? Considering that there is a un-equal potential difference in a parallel circuit?

I haven't work on the numbers yet, wanted to understand all aspects then crunch in the numbers.

 

[NascentOxygen]

Are you drawing the crcuit with three equal resistances yet? The last you posted here still shows only two resistances.

You'll get nowhere fast if you continue pondering an incomplete/incorrect schematic.

I suggest that you don't bother mentioning the phrase "a short circuit" again, there isn't and won't be such a thing in this exercise!

 

[PhiowPhi]

Are you drawing the crcuit with three equal resistances yet? The last you posted here still shows only two resistances.

You'll get nowhere fast if you continue pondering an incomplete/incorrect schematic.

I suggest that you don't bother mentioning the phrase "a short circuit" again, there isn't and won't be such a thing in this exercise!

Yes, I am considering equal resistances. I'm my papers there is, haven't posted one here since you all get the idea.
My understanding of a short-circuit itself is wrong, and if anyone else says there will be one I'd think there would be(which is wrong since I must understand it first).

 

[jim hardy]

Could help clarify my misconception of how this is not a short-circuit?

This image ?

Let's think about leg c for a moment.

If that voltage source is a fixed one,
then ,
as you observed earlier , by KVL leg c has current of 25(or 15) volts divided by resistance of wire in c.
If that resistance is zero then you have a short circuit, for that's what a short circuit is at beginner's level.

But in post #7 you admitted the wire in leg c has resistance, and that's not a short circuit.

So draw a resistor in leg c.
If you want a short circuit, write next to it "0 ohms".
If you do not want a short circuit, write a number other than zero.

Furthermore

Even if c has zero resistance,
you defined your voltage source not as fixed but as induced by ΔΦ/ Δt .
which means magnetic induction,
and induction works both ways
so your leg c has counter emf equal to its inductance L multiplied by Δi/Δt.
which is not a short circuit either.
Lacking any resistance , current will start at zero and increase forever, which is in accordance with ohm's law.

Are you ready to buckle down and tackle this problem yet ?
KIrchoff, Faraday and Ohm are crying out solve it for you, if only you'll let them.

 

[PhiowPhi]

This image ?

Let's think about leg c for a moment.

If that voltage source is a fixed one,
then ,
as you observed earlier , by KVL leg c has current of 25(or 15) volts divided by resistance of wire in c.
If that resistance is zero then you have a short circuit, for that's what a short circuit is at beginner's level.

But in post #7 you admitted the wire in leg c has resistance, and that's not a short circuit.

So draw a resistor in leg c.
If you want a short circuit, write next to it "0 ohms".
If you do not want a short circuit, write a number other than zero.

Furthermore

Even if c has zero resistance,
you defined your voltage source not as fixed but as induced by ΔΦ/ Δt .
which means magnetic induction,
and induction works both ways
so your leg c has counter emf equal to its inductance L multiplied by Δi/Δt.
which is not a short circuit either.
Lacking any resistance , current will start at zero and increase forever, which is in accordance with ohm's law.

Are you ready to buckle down and tackle this problem yet ?
KIrchoff, Faraday and Ohm are crying out solve it for you, if only you'll let them.

Woah, it took me a while to work this up. Sorry for the late response got occupied with other things.
@jim hardy Yes, I'm ready. Thank you for clearing my misunderstanding of short-circuits now I can start to analyse things right.
But before I start my analysis of the current of this circuit I wanted to address on factor that I neglected from the beginning when applying KVL At node (a) of that diagram the voltage is 20V, however, at node(c) the voltage is 25V?

Also, wouldn't KVL be limited in this problem due to failure of "Lumped matter discipline"?

 

[jim hardy]

Lumped Matter Discipline?

Not so long as the dimensions of your circuit are bigger than a wavelength
https://en.wikipedia.org/wiki/Lumped_element_model

Lumped element model
The lumped element model of electronic circuits makes the simplifying assumption that the attributes of the circuit, resistance, capacitance, inductance, and gain, are concentrated into idealized electrical components; resistors, capacitors, and inductors, etc. joined by a network of perfectly conducting wires.

The lumped element model is valid whenever [PLAIN]https://upload.wikimedia.org/math/3/1/3/3132e5ca1aefef695809589e0fdf9d4e.png, where https://upload.wikimedia.org/math/d/8/0/d8006ce4147faea741d82e7d4f4e3c1c.png denotes the circuit's characteristic length, and

denotes the circuit's operating wavelength. Otherwise, when the circuit length is on the order of a wavelength, we must consider more general models, such as the distributed element model (including transmission lines), whose dynamic behaviour is described by Maxwell's equations. Another way of viewing the validity of the lumped element model is to note that this model ignores the finite time it takes signals to propagate around a circuit. Whenever this propagation time is not significant to the application the lumped element model can be used. This is the case when the propagation time is much less than the period of the signal involved. However, with increasing propagation time there will be an increasing error between the assumed and actual phase of the signal which in turn results in an error in the assumed amplitude of the signal. The exact point at which the lumped element model can no longer be used depends to a certain extent on how accurately the signal needs to be known in a given application.

when applying KVL At node (a) of that diagram the voltage is 20V, however, at node(c) the voltage is 25V?

What's the definition of a node?
That blue dot marked C is not the node. The node is everything on the line attached to blue dot C, including power supply negative.
So voltage at blue dot C with respect to power supply negative is zero by definition of "node".
https://en.wikipedia.org/wiki/Node_(circuits)

 

[PhiowPhi]

As always, pleasure reading an informative post by you Jim.
However, I haven't gotten my confusion while applying(KVL) still, here is a better diagram:

Similar to the old circuit(I think a better revised on imo) focusing on my issue, is the applied voltage towards the load 25V or 15V?
Here is another point to consider:

That is what I think the behavior of the induced current($I$) would be.
Just wanted to see the behavior of the EMF's in the circuit in total. When I'm done from the confusion the rest is easy.

 

[jim hardy]

We're back to your paradox.
Look at this part of your circuit. You have conflicting definitions of voltage from top to bottom of it.

What is current capability of an ideal voltage source ? (hint : infinite amps)
What is resistance of an ideal piece of wire ? (hint: zero ohms)
So, what is voltage drop across that wire paralleling your induced 5 volts?
Since V = IR, V = infinite amps X zero ohms
and infinity X zero is indeterminate. not even a number.

KVL says sum of voltages around your red loop equals zero, and 5 + or - an indeterminate non-number does not equal zero.

Devices in parallel must have equal voltage across one another.
5 volts across the ideal voltage source is not equal to zero volts across the ideal wire, nor is it equal to "indeterminate" infinity X zero.

You cannot short circuit an ideal voltage source with an ideal wire.
Attempting to do so is an attempt to force two different voltages onto a single node which violates the concept of a node : same potential everywhere on the node.

If you attempt to do that your equations will deliver impossible results, like 5 = 0.

 

[PhiowPhi]

Clearing out the haze of confusion. Thanks.

 

[meBigGuy]

WOW. I'm so confused about what is so confusing. Assume 3 legs with 100 ohms. Then assume a 5V EMF supply in one leg. It will have no effect on the other two legs because there is a 20V supply that keeps the voltage at a constant across all three legs. The current from the main supply will vary, but the voltage will be constant. If you add a 4th resistor in series with the 20V supply (and all three legs), THEN you will have interactions.

You need to draw a schematic with 4 resistors, 3 resistive legs, and 2 supplies. Then you have something to analyze.

 

[jim hardy]

You need to draw a schematic with 4 resistors, 3 resistive legs, and 2 supplies. Then you have something to analyze.

i hope i addressed the right image.

Let's analyze the last circuit drawn. I've added to it in red...
let us write KVL twice, once around outside path and again around inside path

Outside path:
-20_supply -5_induced +Vload = 0

inside path
-20_supply -0_{across wire} +Vload = 0

Rearranging,
Outside path Vload = 20_supply +5_induced
Vload = 25

Inside path Vload = 20_supply +0_{across wire}
Vload = 20

well,
there's only one Vload, so we can set the equations equal and get result 20 = 25
or
we can subtract the equations
Vload - Vload = 25 - 20
which yields 0 = 5

Kirchoff's law did not fail. It told us that analyzing an impossible circuit yields an impossible result.

MBG is right, one needs a plausible circuit to analyze.

Mr Phi just needs to become more adroit with his "idealized components".

The lumped element model of electronic circuits makes the simplifying assumption that the attributes of the circuit, resistance, capacitance, inductance, and gain, are concentrated into idealized electrical components; resistors, capacitors, and inductors, etc. joined by a network of perfectly conducting wires.

it'll come with practice. We learn from our mistakes - so make lots of 'em.

 

[meBigGuy]

I'd start by removing the short across the VS supply, or turn it into a resistor that's twice the value of the load. Then you will see what is basically going on.

 

[jim hardy]

does this help ?

An ideal wire is a superconductor.
You cannot change flux through a superconducting loop - Lenz's law says current in the loop will become whatever is necessary to keep flux constant.
Faraday tells us constant flux means no dΦ/dt, so no induced voltage.

We see that demonstrated often in levitation experiments.
www.youtube.com/watch?v=4W9HxLOvDus

 

[PhiowPhi]

Well, I have a long way to go. Can't jump things in a matter of month/weeks lol.
But I'll start playing around with circuits soon, I've added that to the list of hobbies, but as an ME undergrad I doubt I'll invest much time into them.