- #1
Casper Hansen
- 13
- 0
Hello
How do I calculate the induced voltage in a passive signal cable that runs parallel to a 1 phase power cable?
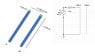
Cable A is the power cable I = 500 A
Cable B passive signal cable
where:
D= 209.65 mm: distance between wires ( center wire to center wire)
r= 10 mm: radios of each wire
f=60 Hz
S=2200 m parallel length
I_rms = 500 A
First i calculate inductance [H/m]
Ls = (u0 / 2 * pi) * ln(D/r) = 6.0857 * 10^-7 [H/m]
Ls_f = Ls * 2 * pi * f => u0 * f * ln(D/r) = 2.294 * 10^-4
Vs = Ls_f * I_rms * sqrt(2) = 0.1622 [V/m]
V = Vs * S = 356.9 V
are the above calculations that the right approach?
My biggest concern is that if I increase the distance between wires S, the inductance increase as well as the induced voltage due to ln(D/r) part in the equation. I can't see why that should be true because the wire (cable B) moves farther away from the source of the B-field (cable A). I thought that the induced voltage would decrease with increased distance of the wires.
How do I calculate the induced voltage in a passive signal cable that runs parallel to a 1 phase power cable?
Cable A is the power cable I = 500 A
Cable B passive signal cable
where:
D= 209.65 mm: distance between wires ( center wire to center wire)
r= 10 mm: radios of each wire
f=60 Hz
S=2200 m parallel length
I_rms = 500 A
First i calculate inductance [H/m]
Ls = (u0 / 2 * pi) * ln(D/r) = 6.0857 * 10^-7 [H/m]
Ls_f = Ls * 2 * pi * f => u0 * f * ln(D/r) = 2.294 * 10^-4
Vs = Ls_f * I_rms * sqrt(2) = 0.1622 [V/m]
V = Vs * S = 356.9 V
are the above calculations that the right approach?
My biggest concern is that if I increase the distance between wires S, the inductance increase as well as the induced voltage due to ln(D/r) part in the equation. I can't see why that should be true because the wire (cable B) moves farther away from the source of the B-field (cable A). I thought that the induced voltage would decrease with increased distance of the wires.