Induced voltage in loop with multiple switches

[artis]

If a current flowing within a loop is interrupted by a switch a spark occurs at some point which is a result of the built up potential across the opening switch contacts due to the stored energy in the magnetic field that was created by the flowing current.

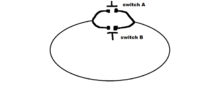
But what happens if I have a loop that has multiple switches as shown in the image attached below, where one switch is always ON (closed) while other switch/es are turned OFF (open) ?
As long as at least one switch is closed/ON the current in the loop continues to flow but what happens at the smaller wires that divide from the main loop and go to each individual switch, does a potential still form across each individual opened/OFF switch because of the current in the smaller wire that divides from the main loop?

 

[Baluncore]

But what happens if I have a loop that has multiple switches as shown in the image attached below, where one switch is always ON (closed) while other switch/es are turned OFF (open) ?

When you flip the switches, you are changing the area of the loop. That repositions the magnetic field lines, the same current keeps flowing, it does not remove the current support for the existing field lines.

 

[artis]

When you flip the switches, you are changing the area of the loop. That repositions the magnetic field lines, the same current keeps flowing, it does not remove the current support for the existing field lines.

I take from what you said that you mean "since current is not interrupted no inductive voltage increase/spike will occur"
And sure if current doesn't change overall the field also doesn't just as you said field lines either spread out or focus in depending on the geometrical location of each switch.

The reason I asked is because although I knew that if current isn't interrupted no inductive EMF will be produced but how about the individual smaller wires that go to each individual switch? the current that is from the place of the common point to the end of each switch, where does that go when that individual switch is opened/switched OFF?

 

[berkeman]

the current that is from the place of the common point to the end of each switch, where does that go when that individual switch is opened/switched OFF?

The other switch shorts out any voltage transient from opening the first switch.

 

[Averagesupernova]

This isn't a well defined question. The answer will vary based on the lengths of various branches in the loops. The way it is drawn it is implied that the wires between the switches and where they join are very short and the remaining wires are significantly longer. In this case, there will be a negligible pulse generated across the switch that opens. As those wires get longer the pulse gets larger.

 

[artis]

This isn't a well defined question. The answer will vary based on the lengths of various branches in the loops. The way it is drawn it is implied that the wires between the switches and where they join are very short and the remaining wires are significantly longer. In this case, there will be a negligible pulse generated across the switch that opens. As those wires get longer the pulse gets larger.

Well that's what I was thinking about, because although the loop as a whole (including the individual branches) never gets switched OFF therefore current can always flow, still the individual branches get switched OFF periodically and that was my questions, is there a separate inductive effect within each smaller branch that is independent from the rest of the circuit and only takes place within the length of the specific individual branch?Because each individual shorter wire also has capacitance and inductance therefore I would guess it has to have an inductive voltage appear across it during a transient , albeit a smaller due to the wire being much shorter and the field much smaller.

 

[TonyStewart]

Let me put a thousand words into a simulation with a Make-before-Break SPDT switch (interactive with mouse click)

Use some 1Vdc source with 0.5mohm resistance.
Add some wire that is perhaps L=1uH/m and R=1mohm /m with two loops, 1 and 100 meter.
The other wire and switch connections are 0.
No stray capacitance or mutual coupling or stray C to ground effects are included but all voltage and currents are monitored . You can add if you want 25 pF/m for Dk=1 wire.

Now manually switch and diagnose all voltages and currents to see if they agree with your logic.

Here are all the results and figure out each or any waveform. Each plot may display a maximum value and some have minimum. with a label that matches or the resistor value.

The plot pane may be dragged up from the edge and then Edit> Center circuit to refit the schematic.
then you may press Reset, Run/Stop, slide speed, and click the center of the SPDT switch.

To change time scale there are two ways:
1) use thumbwheel on top trace when stacked
2) Options> other options> time step size (about 1k samples per time pixel on screen)
3. Simulation time is just like a stripchart recorder speed in slow motion.

You can even change values with the mousewheel hovering over a part or scrap this simulation and make/choose another.

 

[TonyStewart]

But what happens if I have a loop that has multiple switches as shown in the image attached below, where one switch is always ON (closed) while other switch/es are turned OFF (open) ?

Your overlapping make before (both) break, MBB DPST is equivalent to my SPDT MBB switch.
Did you have any more questions?